A new paper is added to the collection of reproducible documents: Seismic data interpolation without iteration using t-x-y streaming prediction filter with varying smoothness
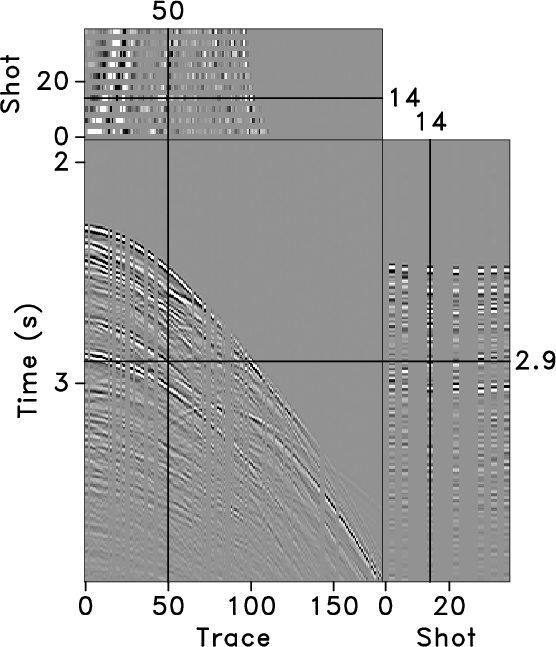

Although there is an increase in the amount of seismic data acquired with wide-azimuth geometry, it is difficult to achieve regular data distributions in spatial directions owing to limitations imposed by the surface environment and economic factor. To address this issue, interpolation is an economical solution. The current state of the art methods for seismic data interpolation are iterative methods. However, iterative methods tend to incur high computational cost which restricts their application in cases of large, high-dimensional datasets. Hence, we developed a two-step non-iterative method to interpolate nonstationary seismic data based on streaming prediction filters (SPFs) with varying smoothness in the time-space domain; and we extended these filters to two spatial dimensions. Streaming computation, which is the kernel of the method, directly calculates the coefficients of nonstationary SPF in the overdetermined equation with local smoothness constraints. In addition to the traditional streaming prediction-error filter (PEF), we proposed a similarity matrix to improve the constraint condition where the smoothness characteristics of the adjacent filter coefficient change with the varying data. We also designed non-causal in space filters for interpolation by using several neighboring traces around the target traces to predict the signal; this was performed to obtain more accurate interpolated results than those from the causal in space version. Compared with Fourier Projection onto a Convex Sets (POCS) interpolation method, the proposed method has the advantages such as fast computational speed and nonstationary event reconstruction. The application of the proposed method on synthetic and nonstationary field data showed that it can successfully interpolate high-dimensional data with low computational cost and reasonable accuracy even in the presence of aliased and conflicting events.
how do we manage interpolated traces to next processes