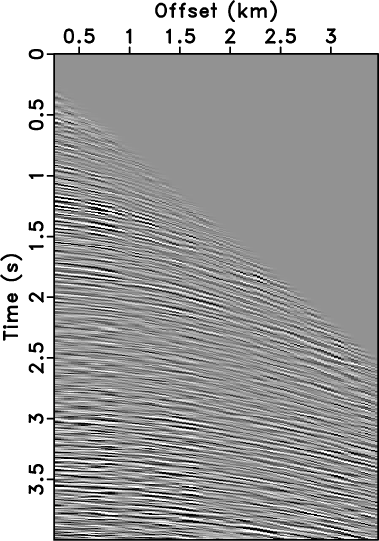
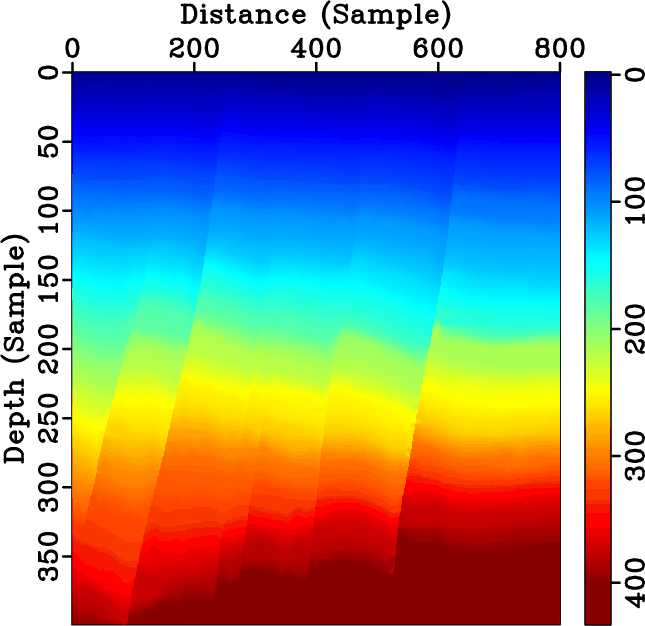
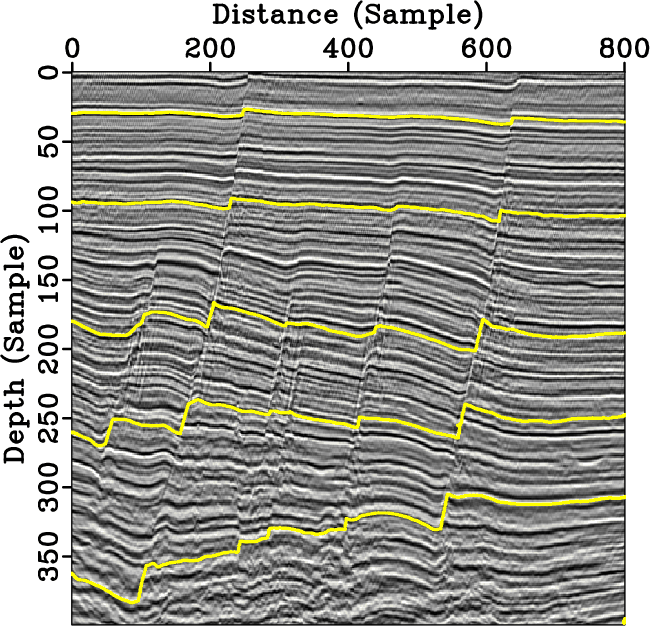
A new paper is added to the collection of reproducible documents: Missing log data interpolation and semiautomatic seismic well ties using data matching techniques
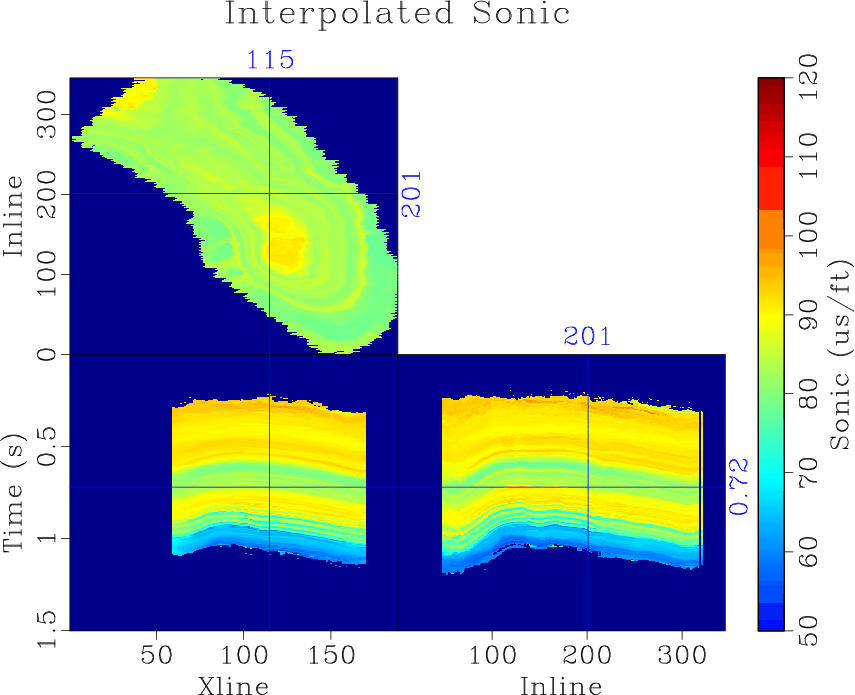
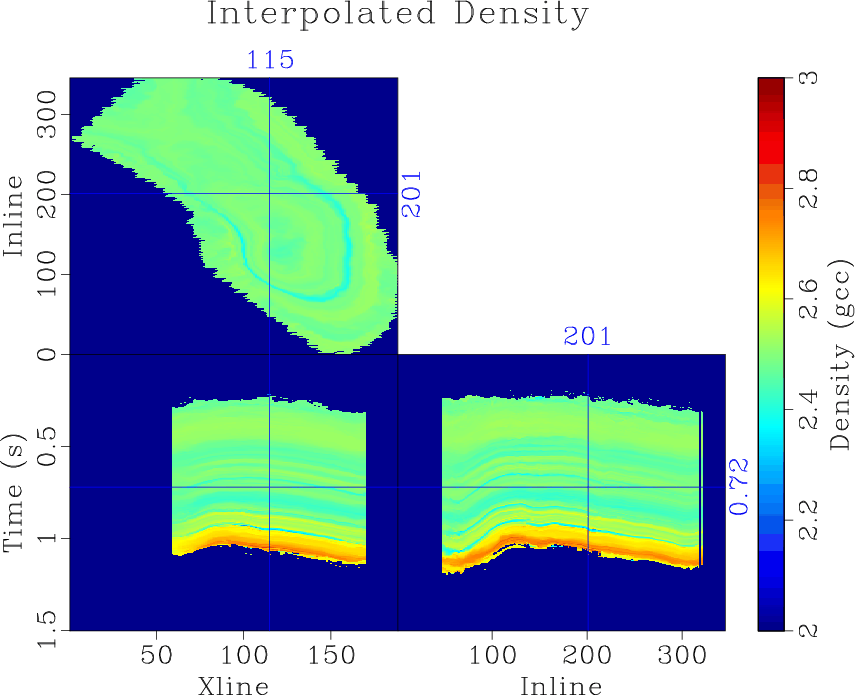
Relating well log data, measured in depth, to seismic data, measured in time, typically requires estimating well log impedance and a time-to-depth relationship using available sonic and density logs. When sonic and density logs are not available, it is challenging to incorporate wells into integrated reservoir studies as the wells cannot be tied to seismic. We propose a workflow to estimate missing well log information, automatically tie wells to seismic data and generate a global well-log property volume using data matching techniques. We first use local similarity scan to align all logs to constant geologic time and interpolate missing well log information. Local similarity is then used to tie available wells with seismic data. Finally, log data from each well is interpolated along local seismic structures to generate global log property volumes. We use blind well tests to verify the accuracy of well-log interpolation and seismic-well ties. Applying the proposed workflow to a 3D seismic dataset with 26 wells achieves consistent and verifiably accurate results.