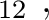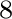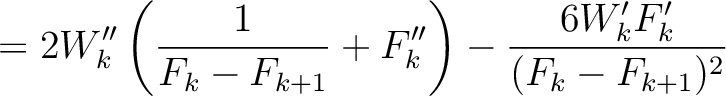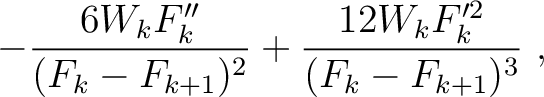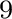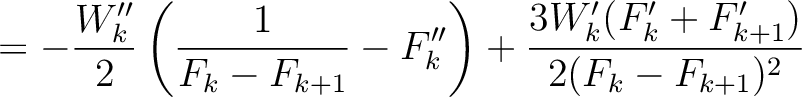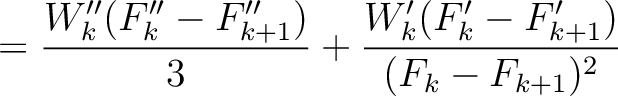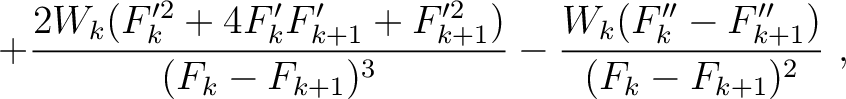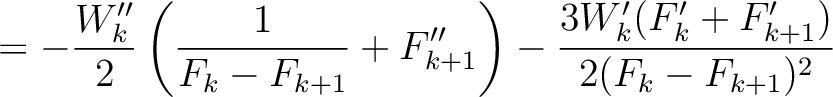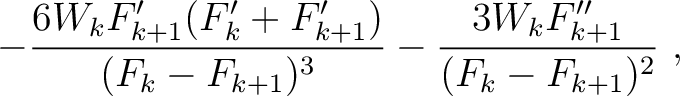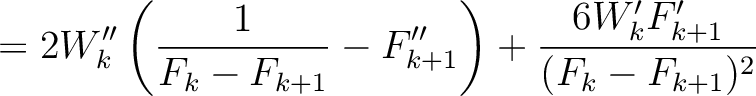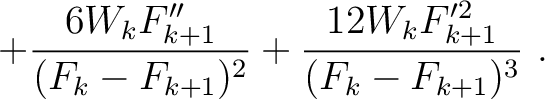In this section, we discuss a possibility of extending our framework to evaluate higher-order one-way traveltime derivatives up to the fourth order. As reviewed in Appendix A, the fourth-order term is particularly important because it can be related to the quartic moveout coefficients for an estimation of anisotropy from reflection traveltime. Nonetheless, we emphasize the possible complications from reflection dispersal that may arise in the study of fourth-order traveltime derivatives for nonhyperbolic moveout (e.g., Pech et al., 2003).
Under similar assumptions used by equation (30), let us consider the two-layer model shown in the left plot of Figure 15 and differentiate the total traveltime (equaiton (37)) with respect to 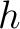 up to the fourth order, which gives
up to the fourth order, which gives
where we highlight the terms that have to be computed recursively for multi-layer media. These include additional second- (
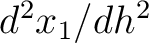 ) and third-order derivatives (
) and third-order derivatives (
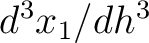 ). In principle, one may therefore, with proper care, further differentiating the Fermat's conditions at different interfaces to obtain the required recursive formulas along the same line as what we did in the derivation of equation (54). An approximation in the same manner as Blias (2006) suitable for the second-order traveltime derivative mentioned in Appendix C may lead to more simplified and manageable expressions.
). In principle, one may therefore, with proper care, further differentiating the Fermat's conditions at different interfaces to obtain the required recursive formulas along the same line as what we did in the derivation of equation (54). An approximation in the same manner as Blias (2006) suitable for the second-order traveltime derivative mentioned in Appendix C may lead to more simplified and manageable expressions.
The one-way traveltime derivatives in each layer that include the effects of lateral heterogeneity can be straightforwardly computed using the current framework (equations (4), (13), and (14)) and we list them here for future references. We limit our consideration for the derivatives of 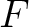 and
and 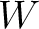 up to the second order in spatial derivatives. These following expressions must be used in conjunction with the exact or approximated recursive formulas that take into account higher-order terms to accumulate the effects of lateral heterogeneity from all layers on reflection or diffraction traveltime. Parameters related to the third-order traveltime derivatives include
up to the second order in spatial derivatives. These following expressions must be used in conjunction with the exact or approximated recursive formulas that take into account higher-order terms to accumulate the effects of lateral heterogeneity from all layers on reflection or diffraction traveltime. Parameters related to the third-order traveltime derivatives include
where we use 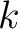 as a dummy index and the heterogeneous terms are given by
Parameters related to the fourth-order traveltime derivatives include
where the heterogeneous terms are given by
as a dummy index and the heterogeneous terms are given by
Parameters related to the fourth-order traveltime derivatives include
where the heterogeneous terms are given by
2024-07-04
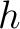 up to the fourth order, which gives
up to the fourth order, which gives
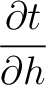
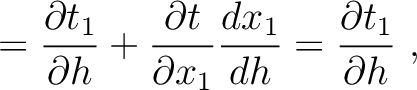
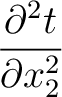
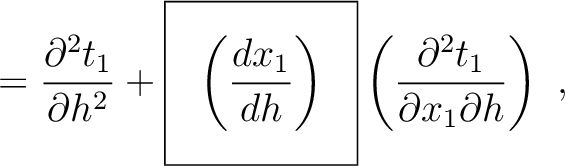
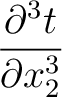
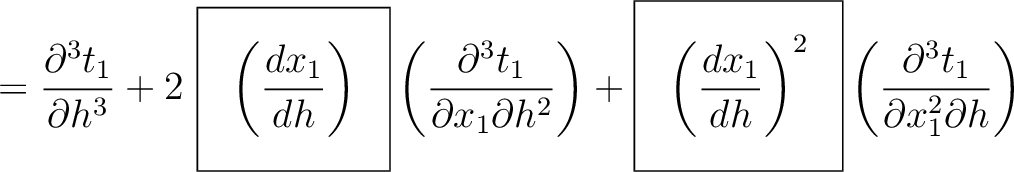
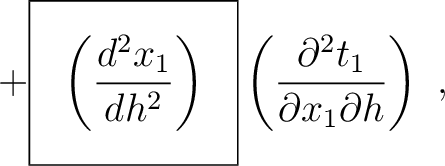
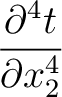
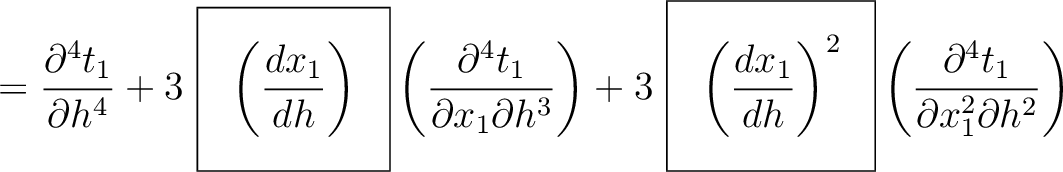
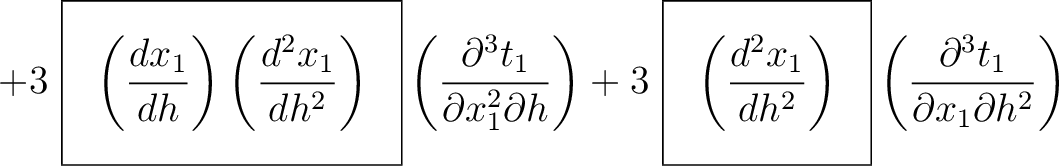
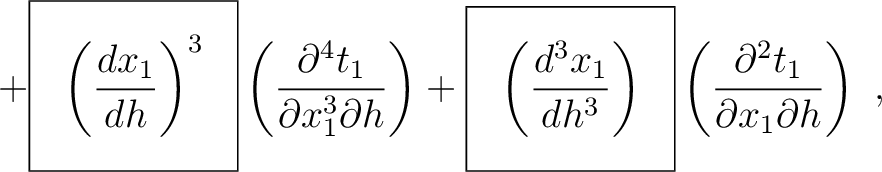
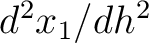 ) and third-order derivatives (
) and third-order derivatives (
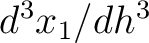 ). In principle, one may therefore, with proper care, further differentiating the Fermat's conditions at different interfaces to obtain the required recursive formulas along the same line as what we did in the derivation of equation (54). An approximation in the same manner as Blias (2006) suitable for the second-order traveltime derivative mentioned in Appendix C may lead to more simplified and manageable expressions.
). In principle, one may therefore, with proper care, further differentiating the Fermat's conditions at different interfaces to obtain the required recursive formulas along the same line as what we did in the derivation of equation (54). An approximation in the same manner as Blias (2006) suitable for the second-order traveltime derivative mentioned in Appendix C may lead to more simplified and manageable expressions.
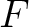 and
and 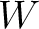 up to the second order in spatial derivatives. These following expressions must be used in conjunction with the exact or approximated recursive formulas that take into account higher-order terms to accumulate the effects of lateral heterogeneity from all layers on reflection or diffraction traveltime. Parameters related to the third-order traveltime derivatives include
up to the second order in spatial derivatives. These following expressions must be used in conjunction with the exact or approximated recursive formulas that take into account higher-order terms to accumulate the effects of lateral heterogeneity from all layers on reflection or diffraction traveltime. Parameters related to the third-order traveltime derivatives include
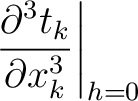
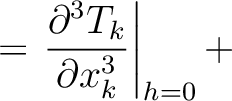 H
H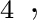
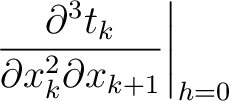
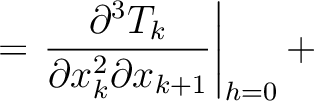 H
H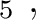
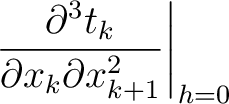
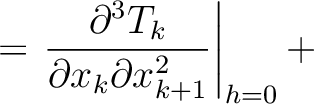 H
H
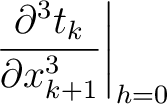
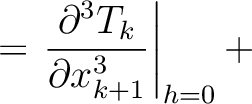 H
H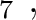
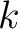 as a dummy index and the heterogeneous terms are given by
as a dummy index and the heterogeneous terms are given by
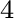
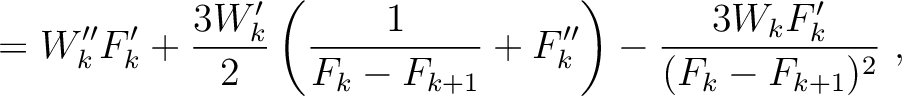
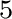
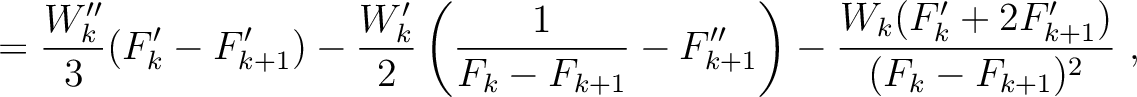
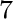
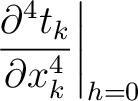
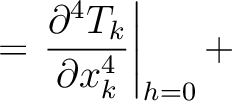 H
H
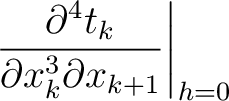
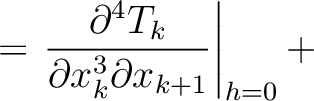 H
H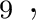
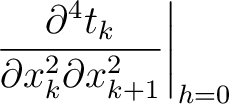
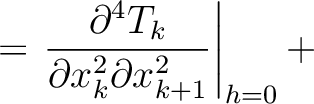 H
H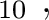
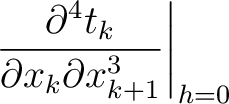
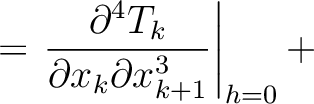 H
H
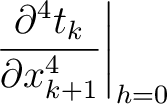
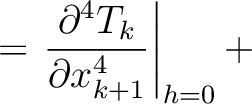 H
H