|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: Appendix C A summation Up: Appendix B Derivation of Previous: Three-layer case
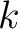 -th interface, there are generally three terms:
-th interface, there are generally three terms:
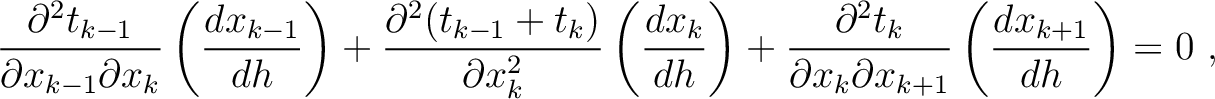 |
(52) |
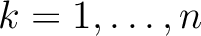 for a medium with
for a medium with  layers. The source at
layers. The source at 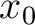 is fixed and therefore,
is fixed and therefore,
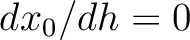 . Moreover, the receiver is located at
. Moreover, the receiver is located at
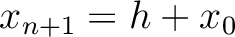 , which leads to
, which leads to
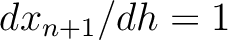 . Therefore, we can derive the following set of equations in the general case of multi-layer media:
. Therefore, we can derive the following set of equations in the general case of multi-layer media:
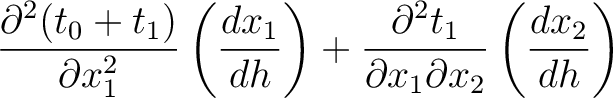 |
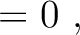 |
(53) |
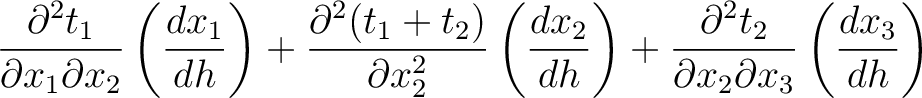 |
 |
|
 |
||
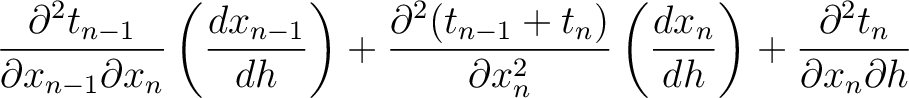 |
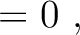 |
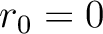 due to
due to
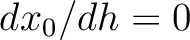 . This newly developed equation is an exact extension of the two-layer case result (equation (42)) to the multi-layer case and is similar to equation (12) in the main text.
. This newly developed equation is an exact extension of the two-layer case result (equation (42)) to the multi-layer case and is similar to equation (12) in the main text.