|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: A recursive formula from Up: Sripanich et al.: Effects Previous: Introduction
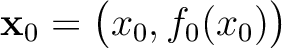 on the interface
on the interface 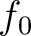 to the receiver
to the receiver
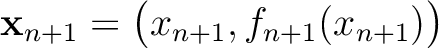 on the interface
on the interface 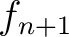 can be written as
where
can be written as
where 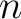 is the number of interfaces and
is the number of interfaces and
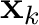 for
for
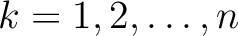 denotes the point of intersection between the ray and
the
denotes the point of intersection between the ray and
the 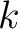 -th interface (Figure 1). Every intersection point
-th interface (Figure 1). Every intersection point
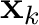 and the receiver
and the receiver
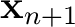 depend on the distance
depend on the distance
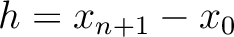 , whereas the source at
, whereas the source at
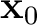 does not. The two-point traveltime
does not. The two-point traveltime 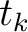 in the
in the 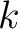 -th layer is given by
where
-th layer is given by
where 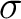 denotes the arc length along the ray between
denotes the arc length along the ray between
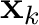 and
and
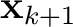 , and
, and 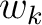 denotes the group slowness (1/group velocity) of the
denotes the group slowness (1/group velocity) of the 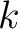 -th layer that depends on
-th layer that depends on 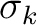 . Assuming that in each layer
. Assuming that in each layer 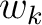 only varies horizontally, equation 2 can be rewritten as
where
only varies horizontally, equation 2 can be rewritten as
where 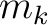 denotes the horizontal coordinate (midpoint direction) and
denotes the horizontal coordinate (midpoint direction) and 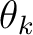 is the angle of the raypath with respect to the vertical. In the following derivation, we assume that the lateral heterogeneity influences are weak and the resulting traveltime perturbations can be computed with respect to a straight raypath in each homogeneous sublayer. Therefore, we assume that
is the angle of the raypath with respect to the vertical. In the following derivation, we assume that the lateral heterogeneity influences are weak and the resulting traveltime perturbations can be computed with respect to a straight raypath in each homogeneous sublayer. Therefore, we assume that 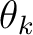 is constant for each
is constant for each 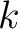 -th layer and rewrite equation 3 as follows (Grechka and Tsvankin, 1999; Lynn and Claerbout, 1982):
-th layer and rewrite equation 3 as follows (Grechka and Tsvankin, 1999; Lynn and Claerbout, 1982):
Equations 1 and 4 serve as the basis for our construction in this study, where we seek the following second-order total one-way traveltime derivative,
evaluated at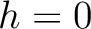 with respect to the reference vertical ray in a 1-D anisotropic medium (Figure 1). We denote the reference intersection point by
with respect to the reference vertical ray in a 1-D anisotropic medium (Figure 1). We denote the reference intersection point by 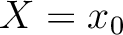 and use `capital letters' to denote quantities evaluated with respect to the reference 1-D anisotropic medium.
and use `capital letters' to denote quantities evaluated with respect to the reference 1-D anisotropic medium.
In consideration of reflection traveltime, equation 5 is related to the NMO velocity as follows:
where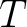 is the one-way zero-offset traveltime from the point
is the one-way zero-offset traveltime from the point
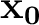 on the reflector to the surface. In the case of diffraction traveltime, equation 5 can be related to time-migration velocity as follows:
where
on the reflector to the surface. In the case of diffraction traveltime, equation 5 can be related to time-migration velocity as follows:
where 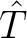 is the one-way vertical traveltime from the point scatterer
is the one-way vertical traveltime from the point scatterer
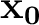 to the surface and we replace
to the surface and we replace 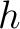 with
with
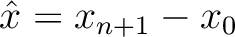 . Even though
. Even though 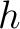 and
and 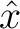 have the same mathematical expression, they represent two different quantities. In case of reflection traveltime, it is common to use
have the same mathematical expression, they represent two different quantities. In case of reflection traveltime, it is common to use 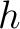 to denote half-offset. On the other hand, in consideration of diffraction traveltime, we use
to denote half-offset. On the other hand, in consideration of diffraction traveltime, we use 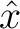 here to denote the distance between the escape location
here to denote the distance between the escape location 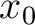 of image ray and any surrounding point
of image ray and any surrounding point 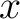 on the surface. We give a brief review on the derivation of equations 6 and 7 in Appendix A.
on the surface. We give a brief review on the derivation of equations 6 and 7 in Appendix A.
Because both NMO velocity (equation 6) for reflection traveltime and time-migration velocity (equation 7) for diffraction traveltime are related to the one-way traveltime derivative of a ray (either normal-incidence or image ray), it is, in principle, sufficient to study the effects from lateral heterogeneity on such derivative of a generic ray travelling between a subsurface position and the surface. We shall adopt this notion in this paper and begin our study by first looking at how the desired second-order one-way traveltime derivative evaluated at the surface (equation 5) is related to the derivatives of 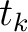 in each sublayer based on the Fermat's principle. This relationship will be used to accumulate the total effects of lateral heterogeneity from all sublayers.
in each sublayer based on the Fermat's principle. This relationship will be used to accumulate the total effects of lateral heterogeneity from all sublayers.