|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: Three-layer case Up: Appendix B Derivation of Previous: Appendix B Derivation of
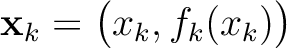 , we may write equation (36) as
We emphasize the simple relationship between
, we may write equation (36) as
We emphasize the simple relationship between 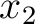 and
and 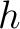 and differentiating equation (37) with respect to
and differentiating equation (37) with respect to 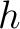 to obtain
to obtain
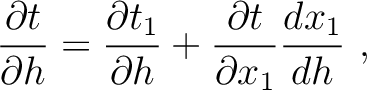 |
(38) |
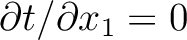 ). Therefore, we have
Further differentiating equation (39) with respect to
). Therefore, we have
Further differentiating equation (39) with respect to 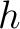 leads to
To evaluate the derivative in equation (40), we need
leads to
To evaluate the derivative in equation (40), we need 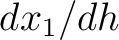 , which can be found from differentiating the Fermat's condition (
, which can be found from differentiating the Fermat's condition (
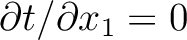 ) with respect to
) with respect to 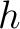 . This leads to
. This leads to
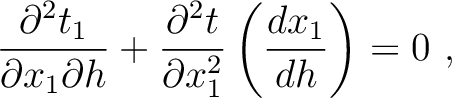 |
(41) |
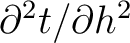 ) to that of the interface below (
) to that of the interface below (
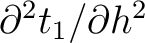 ). All pertaining derivatives in equation (43) can be found from equation (15) in the main text that include the first-order effects from lateral heterogeneity.
). All pertaining derivatives in equation (43) can be found from equation (15) in the main text that include the first-order effects from lateral heterogeneity.
|
|---|
|
2layer
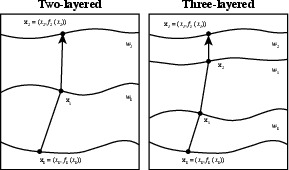
Figure 15. The ray configurations two- and three-layered media as the basis for relating the second-order traveltime derivatives at different interfaces. |
|
|