|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: References Up: Appendix E Possible extension Previous: Two-layer case
 layers, we have
where we need to find
layers, we have
where we need to find
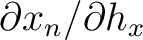 ,
,
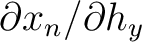 ,
,
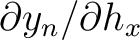 , and
, and
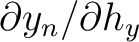 from differentiating the Fermat's principle similar to the previous 2D case. The general form of the linear system of equations at the
from differentiating the Fermat's principle similar to the previous 2D case. The general form of the linear system of equations at the 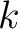 -th interface can be written as
where
-th interface can be written as
where
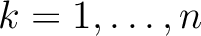 for a medium with
for a medium with  layers. The source at (
layers. The source at (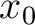 ,
, 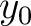 ) is fixed and therefore,
) is fixed and therefore,
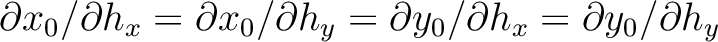 = 0. Moreover, the receiver is located at (
= 0. Moreover, the receiver is located at (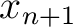 ,
, 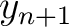 ) = (
) = (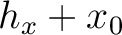 ,
, 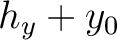 ), which leads to
), which leads to
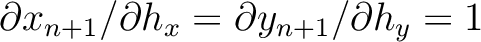 and
and
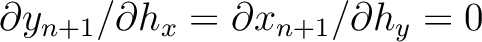 .
.
Looking closer at equation (72), we can see that at the first interface (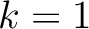 ), we have four equations with eight unknowns:
), we have four equations with eight unknowns:
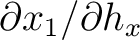 ,
,
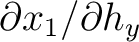 ,
,
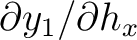 ,
,
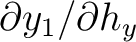 ,
,
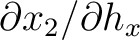 ,
,
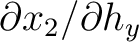 ,
,
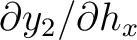 , and
, and
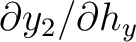 , which is different from the two-layer case in equation (70) that only has four unknowns. In our previous consideration of 2D media (Appendix B), we show that this problem can be circumvented by considering the ratio
, which is different from the two-layer case in equation (70) that only has four unknowns. In our previous consideration of 2D media (Appendix B), we show that this problem can be circumvented by considering the ratio 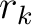 (equation (54)) and formulating a recursive formula. However, it is not immediately apparent how the same strategy can be applied to the system of equations (72) for the 3D media. Therefore, future investigations are required to properly handle this problem and come up with an efficient implementation scheme to analyze influences from lateral heterogeneity on time-processing parameters in 3D media. For example, we may choose to adopt the same strategy as in Appendix D that would allows us to rely on equation (70) and approximately sum individual contributions. Finally, we note that the pertaining one-way traveltime derivatives in each layer — another ingredient apart from the recursive formula— can simply be obtained by extending equations (4), (13), and (14) to 3D to also account for the
(equation (54)) and formulating a recursive formula. However, it is not immediately apparent how the same strategy can be applied to the system of equations (72) for the 3D media. Therefore, future investigations are required to properly handle this problem and come up with an efficient implementation scheme to analyze influences from lateral heterogeneity on time-processing parameters in 3D media. For example, we may choose to adopt the same strategy as in Appendix D that would allows us to rely on equation (70) and approximately sum individual contributions. Finally, we note that the pertaining one-way traveltime derivatives in each layer — another ingredient apart from the recursive formula— can simply be obtained by extending equations (4), (13), and (14) to 3D to also account for the 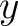 - direction.
- direction.