|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: Multi-layer case Up: Appendix E Possible extension Previous: Appendix E Possible extension
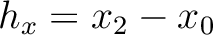 and
and
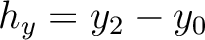 . Equation (67) is the 3D version of equation (37). We can proceed along the same line as before and differentiate equation (67) to obtain
We can see from equation equation (68) that for 3D media, we need to find four derivatives (as opposed to only one in 2D media) in order to relate the traveltime derivatives from one surface to another. To find these four derivatives including
. Equation (67) is the 3D version of equation (37). We can proceed along the same line as before and differentiate equation (67) to obtain
We can see from equation equation (68) that for 3D media, we need to find four derivatives (as opposed to only one in 2D media) in order to relate the traveltime derivatives from one surface to another. To find these four derivatives including
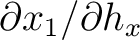 ,
,
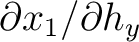 ,
,
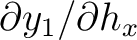 , and
, and
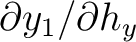 , we differentiate the Fermat's condition for 3D medium:
with respect to
, we differentiate the Fermat's condition for 3D medium:
with respect to 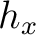 and
and 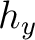 , which leads to the following four conditions:
Equation (70) represents a linear system of four equations to be solved for four unknown derivatives:
, which leads to the following four conditions:
Equation (70) represents a linear system of four equations to be solved for four unknown derivatives:
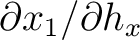 ,
,
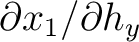 ,
,
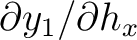 , and
, and
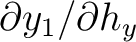 . This is different from equation (42) for the case of 2D media, where we do not need to solve an additional linear system.
. This is different from equation (42) for the case of 2D media, where we do not need to solve an additional linear system.