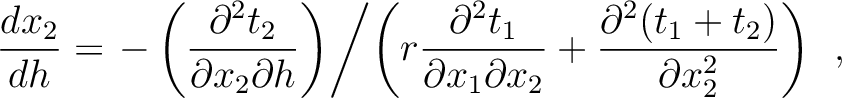Let us now turn to the right plot of Figure 15, which depicts the situation where we have a three-layered medium and the total traveltime is given by
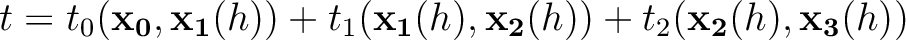 where where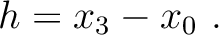 |
(44) |
We can proceed along the same line of argument as in the two-layer case and differentiating the total time with respect to 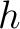 , which leads to
, which leads to
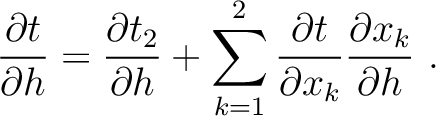 |
(45) |
Again,
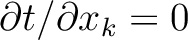 due to the Fermat's principle, we then have
due to the Fermat's principle, we then have
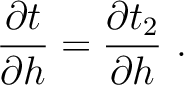 |
(46) |
We further differentiate the expression with respect to 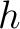 and arrive at
and arrive at
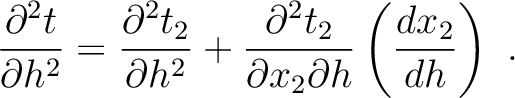 |
(47) |
To find
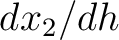 , we differentiate the Fermat's conditions (
, we differentiate the Fermat's conditions (
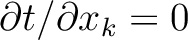 for
for
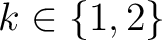 ) in a similar manner as in the two-layer case.
) in a similar manner as in the two-layer case.
- At the first interface (
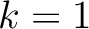 ), the condition
), the condition
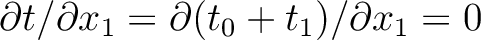 leads to
leads to
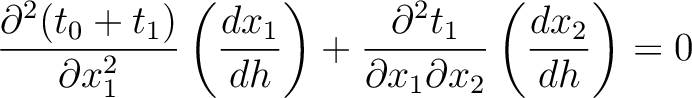 |
(48) |
- At the second interface (
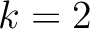 ), the condition
), the condition
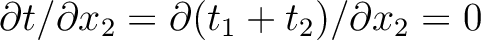 leads to
leads to
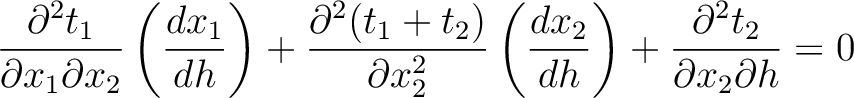 |
(49) |
At this stage, we can see that equations (48) and (49) contain two unknown variables 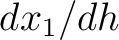 and
and 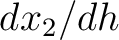 to be solved for. We propose to look at this problem in a specific way that will facilitate an extension to the general multi-layer case. We first rearrange equation (48) into the following form
to be solved for. We propose to look at this problem in a specific way that will facilitate an extension to the general multi-layer case. We first rearrange equation (48) into the following form
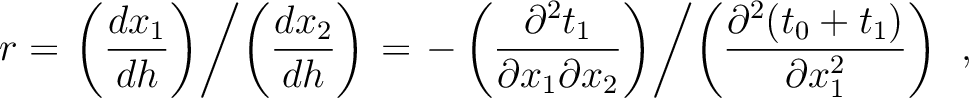 |
(50) |
which is reminiscent of equation (42) for the two-layer case when
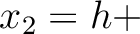 const. Substituting equation (50) into equation (49), we arrive at
const. Substituting equation (50) into equation (49), we arrive at
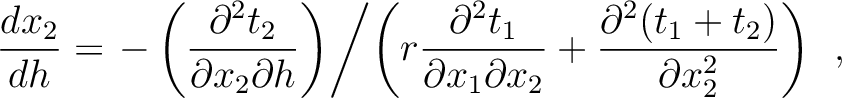 |
(51) |
which can be substituted into equation (47) to evaluate the desired second-order total traveltime derivative.
2024-07-04
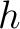 , which leads to
, which leads to
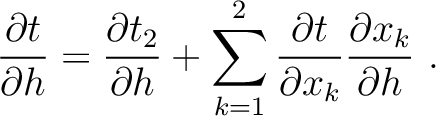
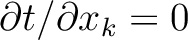 due to the Fermat's principle, we then have
due to the Fermat's principle, we then have
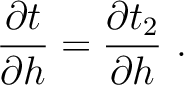
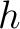 and arrive at
To find
and arrive at
To find
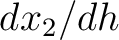 , we differentiate the Fermat's conditions (
, we differentiate the Fermat's conditions (
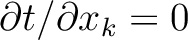 for
for
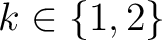 ) in a similar manner as in the two-layer case.
) in a similar manner as in the two-layer case.
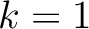 ), the condition
), the condition
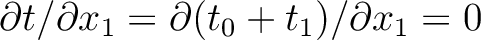 leads to
leads to
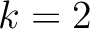 ), the condition
), the condition
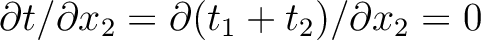 leads to
leads to
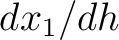 and
and 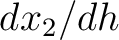 to be solved for. We propose to look at this problem in a specific way that will facilitate an extension to the general multi-layer case. We first rearrange equation (48) into the following form
which is reminiscent of equation (42) for the two-layer case when
to be solved for. We propose to look at this problem in a specific way that will facilitate an extension to the general multi-layer case. We first rearrange equation (48) into the following form
which is reminiscent of equation (42) for the two-layer case when
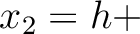 const. Substituting equation (50) into equation (49), we arrive at
const. Substituting equation (50) into equation (49), we arrive at