|
|
|
|
Asymptotic pseudounitary stacking operators |
An interesting example of a stacking operator is the hyperbola summation used for time migration in the post-stack domain. In this case, the summation path is defined as
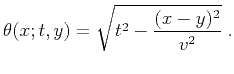 |
(60) |
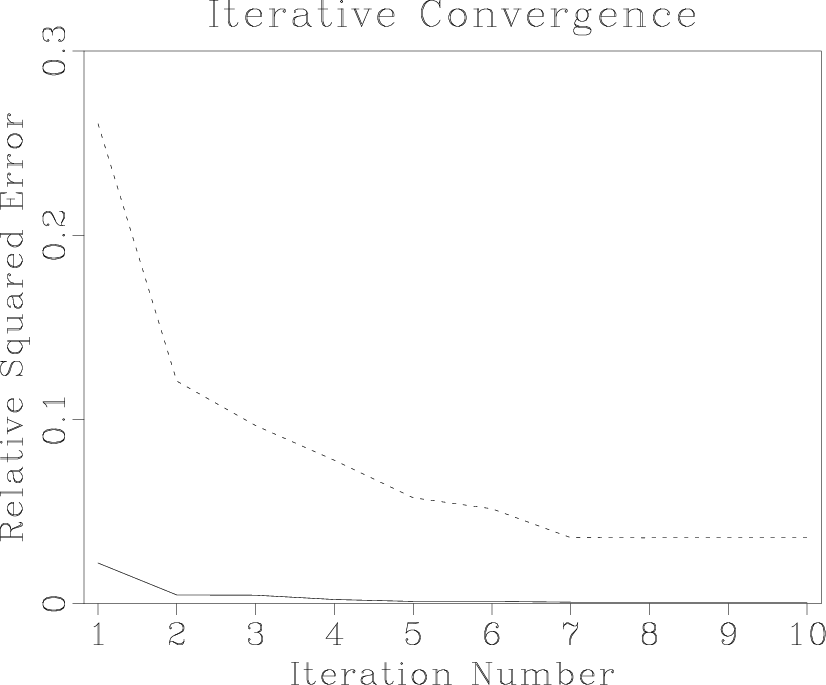
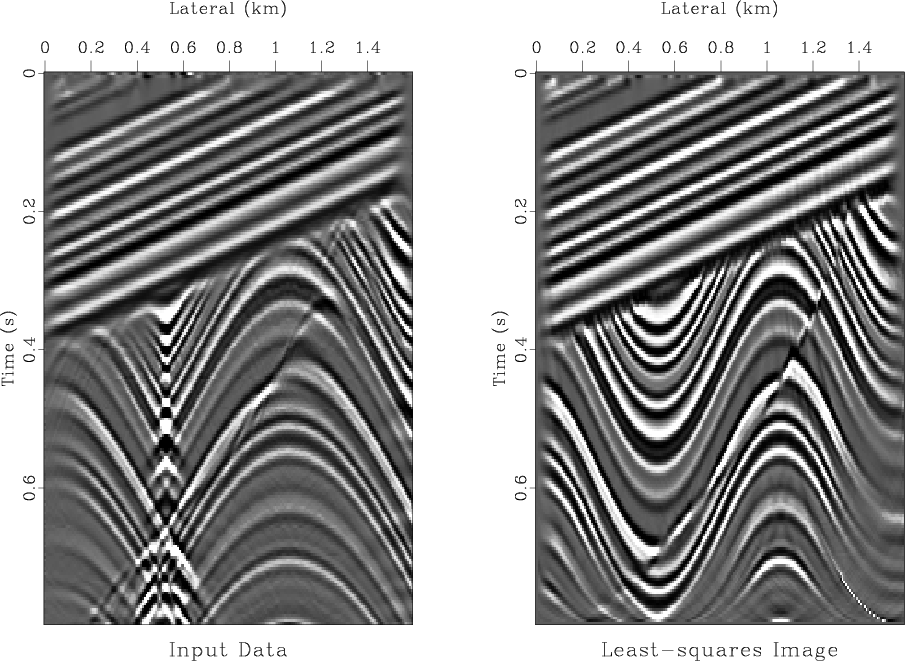
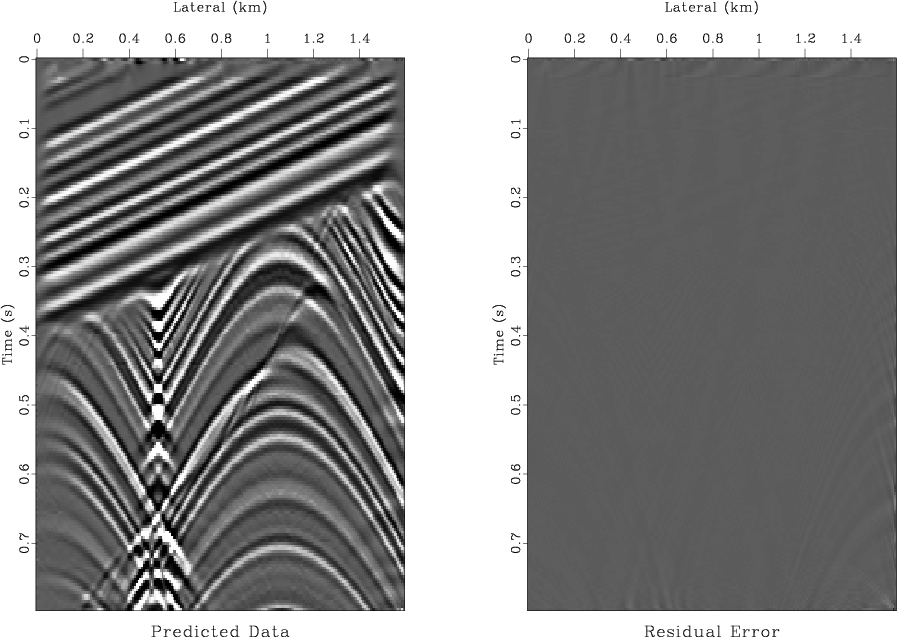
Figure 1 shows the output of a simple numerical test. The synthetic zero-offset section used in this test is shown in the left plot of Figure 2. The data are taken from Claerbout (1995) and correspond to a synthetic reflectivity model, which contains several dipping layers, a fault, and an unconformity. The input zero-offset section is inverted using an iterative conjugate-gradient method and two different weighting schemes: the uniform weighting and the asymptotic pseudo-unitary weighting (67-68). I compare the iterative convergence by measuring the least-squares norm of the data residual error at different iterations. Figure 1 shows that the pseudo-unitary weighting provides a significantly faster convergence. The result of inversion after 10 conjugate-gradient iterations is shown in Figures 2 and 3. The right plot in Figure 2 shows the output of the least-squares migration. Figure 3 shows the corresponding modeled data and the residual error. The latter is very close to zero. Although this example has only a pedagogical value, it clearly demonstrates possible advantages of using asymptotic pseudo-unitary operators in least-squares migration.
|
migiter
Figure 1. Comparison of convergence of the iterative least-squares migration. The dashed line corresponds to the unweighted (uniformly weighted) operator. The solid line corresponds to the asymptotic pseudo-unitary operator. The latter provides a noticeably faster convergence. |
|
|---|---|
|
|
|
|---|
|
migcvv
Figure 2. Input zero-offset section (left) and the corresponding least-squares image (right) after 10 iterations of iterative inversion. |
|
|
|
|---|
|
migrst
Figure 3. The modeled zero-offset (left) and the residual error (right) plotted at the same scale. |
|
|
|
|
|
|
Asymptotic pseudounitary stacking operators |