 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: ASYMPTOTIC PSEUDO-UNITARY OPERATOR PAIR
Up: Asymptotic pseudounitary stacking operators
Previous: ASYMPTOTIC INVERSION: RECONSTRUCTING THE
Least-squares inversion is widely used in practice not only because it
is applicable even when the asymptotic results are unavailable but also
because of its ability to handle finite sampling effects that are
difficult to handle in asymptotic theory (Ronen and Liner, 2000).
The theoretical least-squares inverse of operator (1) has the
well-known form (Tarantola, 1987)
![$\displaystyle \widetilde{M}(z,x)={\bf\widetilde{A}}[S(t,y)]= {\bf\left(A^{T} A\right)^{\dagger} A^{T}}[S(t,y)]\;,$](img41.png) |
(13) |
where 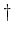 denotes pseudo-inverse, and
the adjoint operator
denotes pseudo-inverse, and
the adjoint operator
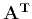 is defined by the dot-product
test:
is defined by the dot-product
test:
![$\displaystyle \left(S(t,y),{\bf A}[M(z,x)]\right) \equiv \left({\bf A^{T}}[S(t,y)],M(z,x)\right)\;.$](img44.png) |
(14) |
With a specified definition of the dot-product, the generalized
inverse minimizes the following quantity, which is the squared  norm of the residual:
norm of the residual:
![$\displaystyle \left(S(t,y)-{\bf A}[M(z,x)], S(t,y)-{\bf A}[M(z,x)]\right)\;.$](img46.png) |
(15) |
In the case of integral operators, a natural definition of the dot-product
is the double integral
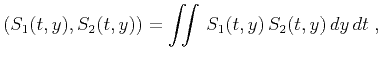 |
(16) |
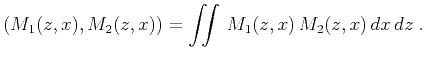 |
(17) |
The notion of the adjoint operator completely depends on the
arbitrarily chosen definition of the dot product and norm in the model
and data spaces. A simple way to change those definitions is to find
some positive weights 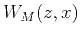 in the model space and
in the model space and 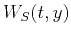 in
the data space that define the dot products as follows:
in
the data space that define the dot products as follows:
To formally define the adjoint of a stacking operator,
let us substitute the definition of the stacking
operator (1) into the dot product
(14), as follows:
![$\displaystyle \left(S(t,y),{\bf A}[M(z,x)]\right) = \int\iint w(x;t,y) M(\theta(x;t,y),x) S(t,y) dx dy dt\;.$](img55.png) |
(20) |
Assuming that the function 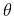 is monotone in
is monotone in 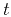
![[*]](icons/footnote.png) , we can change the integration variable
, we can change the integration variable 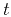 to
to
 and rewrite equation (20) in the form
and rewrite equation (20) in the form
![$\displaystyle \left(S(t,y),{\bf A}[M(z,x)]\right) = \int\iint \widetilde{w}(y;z,x) M(z,x) S(\widehat{\theta}(y;z,x),x) dy dx dz\;,$](img57.png) |
(21) |
where
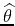 has the same meaning as in equation
(8), and
has the same meaning as in equation
(8), and
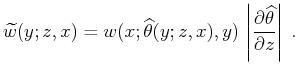 |
(22) |
Comparing equations (21) and (14), we conclude that the adjoint
operator
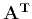 is defined by the equality
is defined by the equality
![$\displaystyle {\bf A^{T}}[S(t,y)]= \int \widetilde{w}(y;z,x) S(\widehat{\theta}(y;z,x),y)\;dy\;.$](img59.png) |
(23) |
Thus we have proven that the continuous adjoint of a
stacking operator is another stacking operator. The adjoint operator
has the same summation path as the asymptotic inverse (8),
which guarantees the correct reconstruction of the kinematics of the
input wavefield. The amplitude (weighting function) of the adjoint
operator is directly proportional to the forward weighting according
to equation (22). The coefficient of proportionality is the
Jacobian of the transformation of the variables 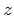 and
and 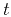 .
.
Similar results have been obtained for particular cases of stacking
operators: velocity transform
(Jedlicka, 1989; Thorson, 1984), Kirchhoff
constant-velocity migration (Ji, 1994), and NMO
(Crawley, 1995). In the appendix, I exemplify an
application of least-squares inversion by reviewing inversion of the
Radon operator and showing that it is precisely equivalent to the
asymptotic result of the previous section.
 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: ASYMPTOTIC PSEUDO-UNITARY OPERATOR PAIR
Up: Asymptotic pseudounitary stacking operators
Previous: ASYMPTOTIC INVERSION: RECONSTRUCTING THE
2013-03-03
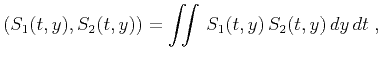
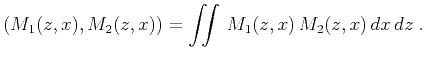
![]() in the model space and
in the model space and ![]() in
the data space that define the dot products as follows:
in
the data space that define the dot products as follows: