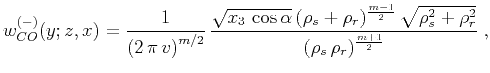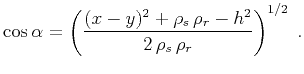|
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: Post-Stack Time Migration
Up: Migration
Previous: 2. Zero-offset migration
In the case of common-offset migration in a general variable-velocity
medium, the weighting function (46) cannot be simplified to a
different form, and all its components need to be calculated
explicitly by dynamic ray tracing (Cerveny and de Castro, 1993). In the
constant-velocity case, we can differentiate the explicit expression
for the summation path
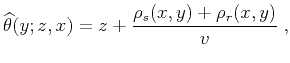 |
(50) |
where  and
and
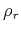 are the lengths of the incident and reflected rays:
are the lengths of the incident and reflected rays:
For simplicity, the vertical component of the midpoint  is set here to zero. Evaluating the second derivative term in formula
(46) for the common-offset geometry leads, after some heavy
algebra, to the expression
is set here to zero. Evaluating the second derivative term in formula
(46) for the common-offset geometry leads, after some heavy
algebra, to the expression
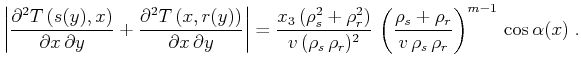 |
(53) |
Substituting (53) into the general formula (46) yields
the weighting function for the common-offset true-amplitude
constant-velocity migration:
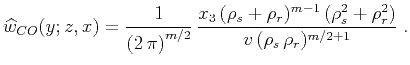 |
(54) |
Equation (54) is similar to the result obtained by
Sullivan and Cohen (1987). In the case of zero offset 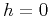 ,
it reduces to equation (49). Note that the value
of
,
it reduces to equation (49). Note that the value
of 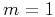 in (54) corresponds to the two-dimensional (cylindric)
waves recorded on the seismic line. A special case is the 2.5-D inversion,
when the waves are assumed to be spherical, while the recording is on a line,
and the medium has cylindric symmetry. In this case, the modeling weighting
function (42) transforms to
(Deregowski and Brown, 1983; Bleistein, 1986)
in (54) corresponds to the two-dimensional (cylindric)
waves recorded on the seismic line. A special case is the 2.5-D inversion,
when the waves are assumed to be spherical, while the recording is on a line,
and the medium has cylindric symmetry. In this case, the modeling weighting
function (42) transforms to
(Deregowski and Brown, 1983; Bleistein, 1986)
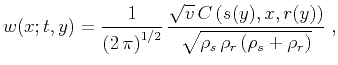 |
(55) |
and the time filter is
 . Combining this result with formula (53)
for
. Combining this result with formula (53)
for 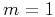 , we obtain the weighting function for the 2.5-D
common-offset migration in a constant velocity medium
(Sullivan and Cohen, 1987):
, we obtain the weighting function for the 2.5-D
common-offset migration in a constant velocity medium
(Sullivan and Cohen, 1987):
 |
(56) |
The corresponding time filter for 2.5-D migration is
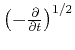 .
.
In the
common-offset case, the pseudo-unitary weighting is defined from
(47) and (53) as follows:
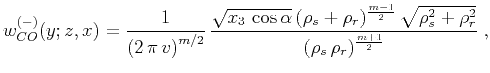 |
(57) |
where
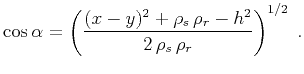 |
(58) |
 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: Post-Stack Time Migration
Up: Migration
Previous: 2. Zero-offset migration
2013-03-03
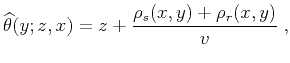


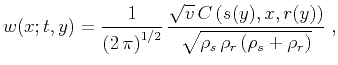
 . Combining this result with formula (53)
for
. Combining this result with formula (53)
for 
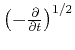 .
.