|
|
|
|
Asymptotic pseudounitary stacking operators |
Mathematical analysis of the inverse problem for operator
(1) shows that only in rare cases can we obtain an
analytically exact inversion. A well-known example is the Radon
transform, which has acquired a lot of different aliases in
geophysical literature: slant stack, tau-p transform, plane wave
decomposition, and controlled directional reception (CDR) transform
(Gardner and Lu, 1991). In this case,
Radon obtained a result similar to the theoretical inversion of operator (1) with the summation path (2) and the weighting function (3) in 1917, but his result was not widely known until the development of computer tomography. According to Radon (1917), the inverse operator has the form
| (5) | |||
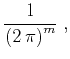 |
(6) |
Extension of Radon's result to the general form of integral operator (1) (generalized Radon transform) is possible via asymptotic analysis of the inverse problem. In the general case, Beylkin (1985) and Goldin (1988) have shown that asymptotic inversion can reconstruct discontinuous parts of the model. These are the parts responsible for the asymptotic behavior of the model at high frequencies. Since the discontinuities are associated with wavefronts and reflection events at seismic sections, there is a certain correspondence between asymptotic inversion and such standard goals of seismic data processing as kinematic equivalence and amplitude preservation.
The main theorem of asymptotic inversion can be formulated as follows
(Goldin, 1988). The leading-order discontinuities in ![]() are
reconstructed by an integral operator of the form
are
reconstructed by an integral operator of the form
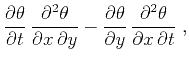 |
(11) | ||
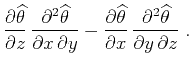 |
(12) |
 , and the asymptotic inverse coincides with the
exact inversion.
, and the asymptotic inverse coincides with the
exact inversion.
|
|
|
|
Asymptotic pseudounitary stacking operators |