 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: EXAMPLES
Up: Asymptotic pseudounitary stacking operators
Previous: LEAST-SQUARES INVERSION AND ADJOINT
According to the theory of asymptotic inversion, briefly reviewed in
the first part of this paper, the weighting function of the
asymptotically inverse operator is inversely proportional to the
weighting of the forward operator. On the other hand, the weighting in
the adjoint is directly proportional to the forward
weighting. This difference allows us to define a hybrid pair of
operators that possess both the property of being adjoint and the
property of being asymptotic inverse. It is appropriate to call a pair
of operators defined in this way asymptotic pseudo-unitary. The
definition of asymptotic pseudo-unitary operators follows directly
from the combination of definitions (8) and
(23). Splitting the derivative operator  in
(8) into the product of two operators, we can write the
forward operator as
in
(8) into the product of two operators, we can write the
forward operator as
![$\displaystyle S(t,y)= {\bf A}\left[M(z,x)\right]= \int w^{(+)}(x;t,y) \vert{\bf D}\vert^{m/2} M(\theta(x;t,y),x) dx$](img60.png) |
(24) |
and its asymptotic pseudo-unitary adjoint as
![$\displaystyle \widetilde{M}(z,x)={\bf\widetilde{A}}[S(t,y)]= \vert{\bf D}\vert^{m/2}\;\int w^{(-)}(y;z,x) S(\widehat{\theta}(y;z,x),y)\;dy\;.$](img61.png) |
(25) |
According to equation (10),
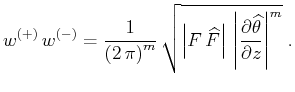 |
(26) |
According to equation (22),
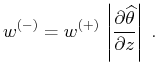 |
(27) |
Combining equations (26) and (27) uniquely determines
both weighting functions, as follows:
Equations (28) and (29) complete the definition of
asymptotic pseudo-unitary operator pair.
The notion of pseudo-unitary operators is directly applicable in the
situations where we can arbitrarily construct both forward and inverse
operators. One example of such a situation is the velocity transform
considered in the next section of this paper. In the more common
case, the forward operator is strictly defined by the physics of a
problem. In this case, we can include asymptotic inversion in the
iterative least-squares inversion by means of preconditioning
(Lambaré et al., 1992; Jin et al., 1992). The linear preconditioning operator should
transform the forward stacking-type operator to the form
(24) with the weighting function (28).
Theoretically, this form of preconditioning should lead to the fastest
convergence of the iterative least-squares inversion with respect to
the high-frequency parts of the model.
If the forward pseudo-unitary operator
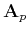 can be related to
the forward modeling operator
can be related to
the forward modeling operator
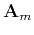 as
as
 , where
, where
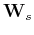 and
and
 are weighting operators in the data and model domains
correspondingly, then preconditioning simply amounts to replacing the
least-squares equation
are weighting operators in the data and model domains
correspondingly, then preconditioning simply amounts to replacing the
least-squares equation
![$\displaystyle S \approx \mathbf{A}_m [M]$](img73.png) |
(30) |
with the equation
![$\displaystyle \mathbf{W}_s [S] \approx \mathbf{W}_s \mathbf{A}_m \mathbf{W}_m [P] = \mathbf{A}_p [P]\;,$](img74.png) |
(31) |
where 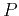 is the preconditioned model. The advantage of using
equation (31) is in the the fact that the normal operator
is the preconditioned model. The advantage of using
equation (31) is in the the fact that the normal operator
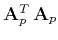 is closer (asymptotically) to identity and
therefore should be easier to invert than the original operator
is closer (asymptotically) to identity and
therefore should be easier to invert than the original operator
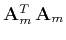 in the least-squares solution (13).
in the least-squares solution (13).
 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: EXAMPLES
Up: Asymptotic pseudounitary stacking operators
Previous: LEAST-SQUARES INVERSION AND ADJOINT
2013-03-03
![]() can be related to
the forward modeling operator
can be related to
the forward modeling operator
![]() as
as
![]() , where
, where
![]() and
and
![]() are weighting operators in the data and model domains
correspondingly, then preconditioning simply amounts to replacing the
least-squares equation
are weighting operators in the data and model domains
correspondingly, then preconditioning simply amounts to replacing the
least-squares equation