As I will illustrate in later chapters, the crucial part of data
regularization problems is in the choice and implementation of the
regularization operator
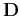
or the corresponding
preconditioning operator
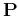
. The choice of the forward
modeling operator
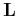
is less critical. In this chapter, I
discuss the nature of forward interpolation, which has been one of the
traditional subjects in computational mathematics.
Wolberg (1990)
presents a detailed review of different conventional approaches. I
discuss a simple mathematical theory of interpolation from a regular
grid and derive the main formulas from a very general idea of function
bases.
Forward interpolation plays only a supplementary role in this
dissertation, but it has many primary applications, such as trace
resampling, NMO, Kirchhoff and Stolt migrations, log-stretch, and
radial transform, in seismic data processing and imaging. Two simple
examples appear at the end of this chapter.