Next: Asymptotically pseudo-unitary operators as
Up: Fomel: Forward interpolation
Previous: Discrete Fourier basis
Of course, the linear theory is not limited to discrete grids. It is
interesting to consider the continuous case because of its connection
to the linear integral operators commonly used in seismic imaging.
Indeed, in the continuous case, linear decomposition (8)
takes the form of the integral operator
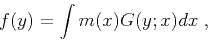 |
(25) |
where 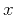 is a continuous analog of the discrete coefficient
is a continuous analog of the discrete coefficient 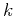 in
(8), the continuous function
in
(8), the continuous function 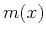 is analogous to the
coefficient
is analogous to the
coefficient 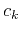 , and
, and 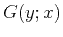 is analogous to one of the basis
functions
is analogous to one of the basis
functions 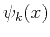 . The linear integral operator in
(25) has a mathematical form similar to the form of
well-known integral imaging operators, such as Kirchhoff migration or
``Kirchhoff'' DMO. Function
. The linear integral operator in
(25) has a mathematical form similar to the form of
well-known integral imaging operators, such as Kirchhoff migration or
``Kirchhoff'' DMO. Function 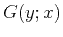 in this case represents the
Green's function (impulse response) of the imaging operator. Linear
decomposition of the data into basis functions means decomposing it
into the combination of impulse responses (``hyperbolas'').
in this case represents the
Green's function (impulse response) of the imaging operator. Linear
decomposition of the data into basis functions means decomposing it
into the combination of impulse responses (``hyperbolas'').
In the continuous case, equation (15) transforms to
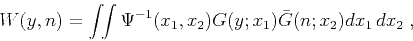 |
(26) |
where
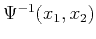 refers to the inverse of the ``matrix''
operator
refers to the inverse of the ``matrix''
operator
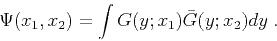 |
(27) |
When the linear operator, defined by equation (25), is
unitary,
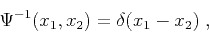 |
(28) |
and equation (26) simplifies to the single integral
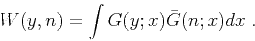 |
(29) |
With respect to seismic imaging operators, one can recognize in the
interpolation operator (29) the generic form of azimuth moveout
(Biondi et al., 1996), which is derived either as a cascade of adjoint
(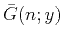 ) and forward (
) and forward (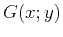 ) DMO or as a cascade of migration
(
) DMO or as a cascade of migration
(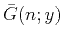 ) and modeling (
) and modeling (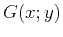 )
(Fomel and Biondi, 1995; Biondi et al., 1998). In the first case, the
intermediate variable
)
(Fomel and Biondi, 1995; Biondi et al., 1998). In the first case, the
intermediate variable 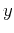 corresponds to the space of zero-offset data cube.
In the second case, it corresponds to a point in the subsurface.
corresponds to the space of zero-offset data cube.
In the second case, it corresponds to a point in the subsurface.
Subsections
Next: Asymptotically pseudo-unitary operators as
Up: Fomel: Forward interpolation
Previous: Discrete Fourier basis
2014-02-21