|
|
|
|
Forward interpolation |
Mathematical interpolation theory considers a function ![]() , defined on
a regular grid
, defined on
a regular grid ![]() . The problem is to find
. The problem is to find ![]() in a continuum that
includes
in a continuum that
includes ![]() . I am not defining the dimensionality of
. I am not defining the dimensionality of ![]() and
and ![]() here
because it is not essential for the derivations. Furthermore, I am
not specifying the exact meaning of ``regular grid,'' since it will
become clear from the analysis that follows. The function
here
because it is not essential for the derivations. Furthermore, I am
not specifying the exact meaning of ``regular grid,'' since it will
become clear from the analysis that follows. The function ![]() is
assumed to belong to a Hilbert space with a defined dot product.
is
assumed to belong to a Hilbert space with a defined dot product.
If we restrict our consideration to a linear case, the desired
solution will take the following general form
Equality (2) is necessary to assure that the interpolation of a single spike at some point
This property is the normalization condition. Formula (3) assures that interpolation of a constant function
One classic example of the interpolation weight ![]() is the
Lagrange polynomial, which has the form
is the
Lagrange polynomial, which has the form
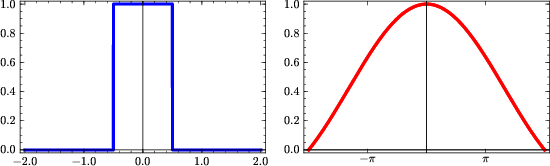
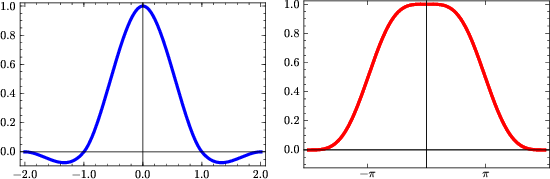
Because of their simplicity, the nearest-neighbor and linear interpolation methods are very practical and easy to apply. Their accuracy is, however, limited and may be inadequate for interpolating high-frequency signals. The shapes of interpolants (5) and (6) and their spectra are plotted in Figures 1 and 2. The spectral plots show that both interpolants act as low-pass filters, preventing the high-frequency energy from being correctly interpolated.
|
|---|
|
nnint
Figure 1. Nearest-neighbor interpolant (left) and its spectrum (right). |
|
|

|
|---|
|
linint
Figure 2. Linear interpolant (left) and its spectrum (right). |
|
|
The Lagrange interpolants of higher order correspond to more
complicated polynomials. Another popular practical approach is cubic
convolution (Keys, 1981). The cubic convolution interpolant is a local
piece-wise cubic function:
|
|---|
|
ccint
Figure 3. Cubic-convolution interpolant (left) and its spectrum (right). |
|
|
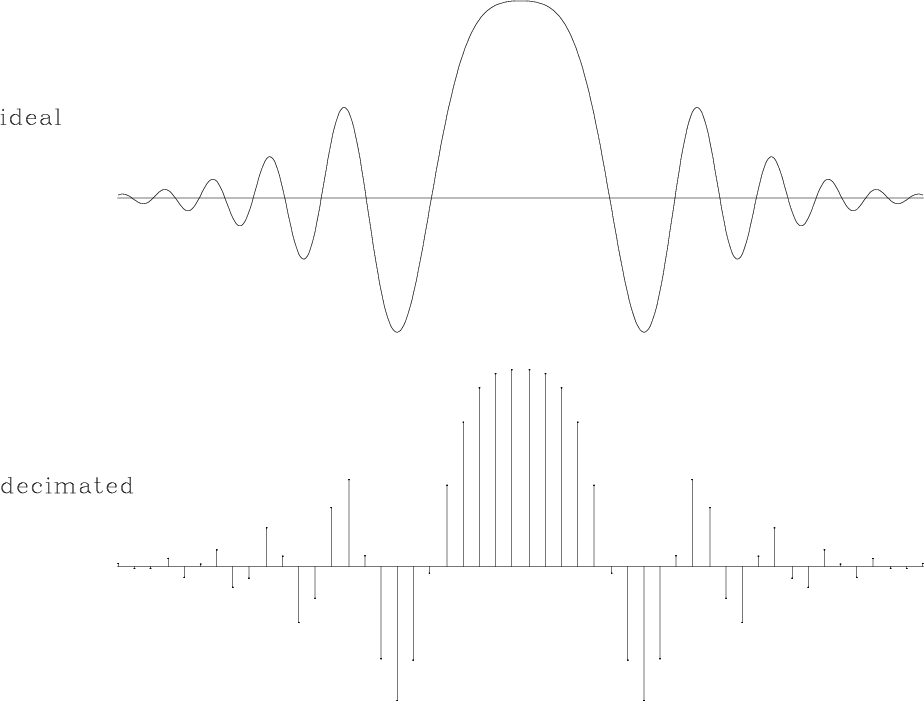
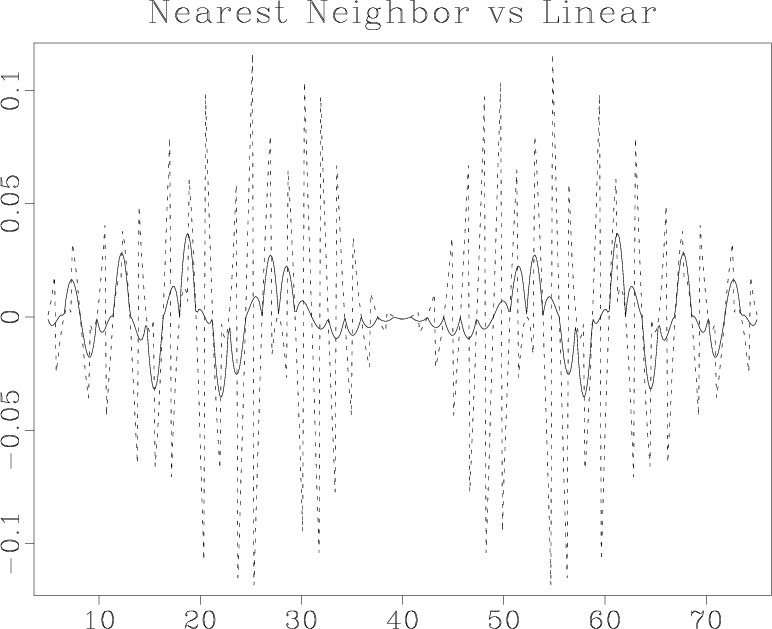
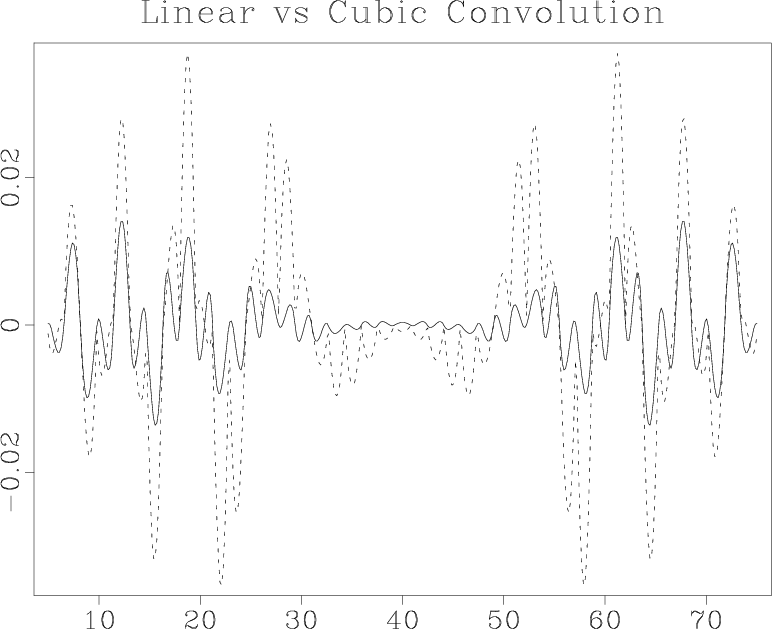
I compare the accuracy of different forward interpolation methods on a one-dimensional signal shown in Figure 4. The ideal signal has an exponential amplitude decay and a quadratic frequency increase from the center towards the edges. It is sampled at a regular 50-point grid and interpolated to 500 regularly sampled locations. The interpolation result is compared with the ideal one. Figures 5 and 6 show the interpolation error steadily decreasing as we proceed from 1-point nearest-neighbor to 2-point linear and 4-point cubic-convolution interpolation. At the same time, the cost of interpolation grows proportionally to the interpolant length.
|
chirp
Figure 4. One-dimensional test signal. Top: ideal. Bottom: sampled at 50 regularly spaced points. The bottom plot is the input in a forward interpolation test. |
|
|---|---|
|
|
|
binlin
Figure 5. Interpolation error of the nearest-neighbor interpolant (dashed line) compared to that of the linear interpolant (solid line). |
|
|---|---|
|
|
|
lincub
Figure 6. Interpolation error of the linear interpolant (dashed line) compared to that of the cubic convolution interpolant (solid line). |
|
|---|---|
|
|
|
|
|
|
Forward interpolation |