Next: Continuous case and seismic
Up: Interpolation with Fourier basis
Previous: Continuous Fourier basis
Assuming that the range of the variable 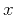 is limited in the interval
from
is limited in the interval
from 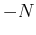 to
to 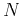 , the discrete Fourier basis (Fast Fourier
Transform) employs a set of orthonormal periodic functions
, the discrete Fourier basis (Fast Fourier
Transform) employs a set of orthonormal periodic functions
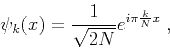 |
(23) |
where the discrete frequency index 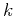 also ranges, according to the
Nyquist sampling criterion, from
also ranges, according to the
Nyquist sampling criterion, from 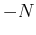 to
to 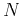 . The interpolation
function is computed from equation (15) to be
. The interpolation
function is computed from equation (15) to be
An interpolation function equivalent to (24) has been
found by Muir (Popovici et al., 1993,1996; Lin et al., 1993). It can
be considered a tapered version of the sinc interpolant
(21) with smooth tapering function
Unlike most other tapered-sinc interpolants, Muir's interpolant
(24) satisfies not only the obvious property
(2), but also properties (3) and
(19), where the interpolation function 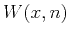 should
be set to zero for
should
be set to zero for 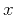 outside the range from
outside the range from 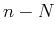 to
to 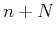 . The
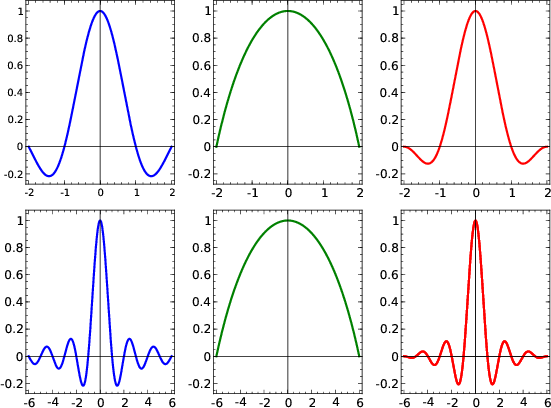
form of this function is shown in Figure 11.
. The
form of this function is shown in Figure 11.
|
|---|
ma-sinc
Figure 11. The left plots show the sinc interpolation
function. Note the slow decay in 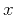 . The middle shows the
effective tapering function of Muir's interpolation; the right is
Muir's interpolant. The top is for . The middle shows the
effective tapering function of Muir's interpolation; the right is
Muir's interpolant. The top is for 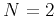 (5-point interpolation);
the bottom, (5-point interpolation);
the bottom,  (13-point interpolation). (13-point interpolation).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[sage]](icons/sage.png)
|
|---|
The development of the mathematical wavelet theory (Daubechies, 1992) has
opened the door to a whole universe of orthonormal function bases,
different from the Fourier basis. The wavelet theory should find many
useful applications in geophysical data interpolation, but exploring
this interesting opportunity would go beyond the scope of the present
work.
The next section carries the analysis to the continuum and compares
the mathematical interpolation theory with the theory of seismic
imaging.
Next: Continuous case and seismic
Up: Interpolation with Fourier basis
Previous: Continuous Fourier basis
2014-02-21
![]() is limited in the interval
from
is limited in the interval
from ![]() to
to ![]() , the discrete Fourier basis (Fast Fourier
Transform) employs a set of orthonormal periodic functions
, the discrete Fourier basis (Fast Fourier
Transform) employs a set of orthonormal periodic functions
![\begin{displaymath}
\frac{\pi (x - n)/2N}{\tan\left[\pi (x - n)/2N\right]}\;.
\end{displaymath}](img68.png)
