 |
 |
 |
 | Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |  |
![[pdf]](icons/pdf.png) |
Next: Numerical examples
Up: Theory
Previous: Low-rank approximation
The proposed method is well-suited for applications to elastic imaging and inversion using multi-component seismic data. In this section, we derive the energy-norm imaging condition using analytical wavefield, and show its connection to wave-mode decomposition.
The energy norm with respect to a SPD matrix
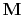 can be defined as:
can be defined as:
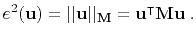 |
(34) |
In the acoustic case, the imaging condition based on the energy-norm is also referred to as the impedance sensitivity kernal (Zhu et al., 2009) or the inverse scattering imaging condition (Whitmore and Crawley, 2012):
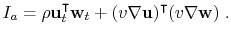 |
(35) |
For general elastic media, the energy norm imaging condition can be expressed as (Kiyashchenko et al., 2007; Rocha et al., 2016)
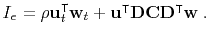 |
(36) |
Using the analytic wavefield, equation 36 becomes
![$\displaystyle I_e = \rho ( \mathbf{u}_t^\intercal \mathbf{w}_t + \mathbf{u}^\in...
...hscr{R}\left[ \rho (\Phi \hat{\mathbf{u}})^*(\Phi \hat{\mathbf{w}}) \right] \;,$](img184.png) |
(37) |
where
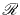 represents the operator of taking the real part. In a locally homogeneous medium, equation 37 can be expressed as
represents the operator of taking the real part. In a locally homogeneous medium, equation 37 can be expressed as
![$\displaystyle I_e = \mathscr{R}\left[ \mathscr{F}^{-1} \left[ \rho \hat{\mathbf{u}}^* \mathbf{A}\hat{\mathbf{w}} \right] \right] \;,$](img186.png) |
(38) |
where
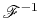 represents inverse spatial Fourier transform.
represents inverse spatial Fourier transform.
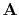 is SPD and has the eigenvalue decomposition as equation 13, and the part in the wavenumber domain of equation 38 can be further expanded as
is SPD and has the eigenvalue decomposition as equation 13, and the part in the wavenumber domain of equation 38 can be further expanded as
Equation 39 corresponds to the summation of the image produced by three pure wave-mode reflections (P-P, S1-S1 and S2-S2 images) using the formula prescribed in equations 35. Therefore, the proposed framework provides the possibility of individually accessing the contribution of each wave-mode in the elastic energy-norm imaging condition, in addition to outputing their summation.
The imaging condition prescribed in equation 38 is the cross-correlation of two positive-frequency analytical wavefields. This corresponds to the back-scattering part of the wavefield. If one instead performs cross-correlation between two wavefield with opposite signs of frequency, e.g.
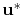 only contains negative frequency and
only contains negative frequency and
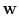 only contains positive frequency, it will lead to a different forward-scattering imaging condition
only contains positive frequency, it will lead to a different forward-scattering imaging condition
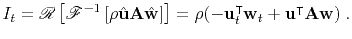 |
(40) |
The forward-scattering imaging condition corresponds to the tomographic correlation between two wavefields. It is conventionally treated as low-frequency noise in RTM, but is what FWI needs for performing low-frequency updates in the velocity gradient Ramos-Martinez et al. (2016); Díaz and Sava (2012,2013). Equation 40 can also be expanded in a similar fashion as equation 39 to access individual contributions from each wave mode.
It is important to note that the inverse- and forward-scattering imaging conditions using scalar and vector analytical wavefields discussed in this section are not restricted to one-step wave extrapolation. There are different ways of obtaining an analytical wavefield using conventional finite-different or pseudo-spectral wave extrapolation, for example, by separately propagating a wavefield using a Hilbert-transformed source wavelet (Hu et al., 2016; Shen and Albertin, 2015) and use it as the imaginary part of the analytical wavefield.
 |
 |
 |
 | Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |  |
![[pdf]](icons/pdf.png) |
Next: Numerical examples
Up: Theory
Previous: Low-rank approximation
2018-11-16
![]() can be defined as:
can be defined as:
![]() only contains negative frequency and
only contains negative frequency and
![]() only contains positive frequency, it will lead to a different forward-scattering imaging condition
only contains positive frequency, it will lead to a different forward-scattering imaging condition