|
|
|
|
Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |
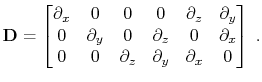 |
(11) |
In the Fourier (wavenumber) domain, the homogeneous
![]() takes the form
takes the form
![]() after
after ![]() cancels the negative sign, i.e.,
cancels the negative sign, i.e.,
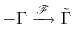 .
For example, the Christoffel matrix
.
For example, the Christoffel matrix
![]() in the case of orthorhombic anisotropy takes the form:
in the case of orthorhombic anisotropy takes the form:
The square root matrix ![]() is analogous to the phase function in the acoustic case, and corresponds to the angular frequency
is analogous to the phase function in the acoustic case, and corresponds to the angular frequency ![]() according to the dispersion relation. Since the matrix
according to the dispersion relation. Since the matrix
![]() is symmetric positive definite (SPD), it can be diagonalized with its eigenvalues corresponding to the square of phase velocity of separate wave modes and its orthogonal eigenvectors corresponding to the polarization directions:
is symmetric positive definite (SPD), it can be diagonalized with its eigenvalues corresponding to the square of phase velocity of separate wave modes and its orthogonal eigenvectors corresponding to the polarization directions:
In 3D, we can transform the input vector in the wavenumber domain
![]() . To apply the Fourier integral operator, we omit the pair of forward and backward Fourier transforms and formally write
. To apply the Fourier integral operator, we omit the pair of forward and backward Fourier transforms and formally write
Using the form of equation 9, we can also define the backward time extrapolator
Expanding the wave extrapolation operator in the form of equations 17 and 22 reveals a simple relationship between wave propagation and wave mode decomposition. In the one-step formulation, each individual term contained in each element of
![]() is essentially a sequence of wave-mode decomposition, phase shift and recomposition. For example, the action of the first term in
is essentially a sequence of wave-mode decomposition, phase shift and recomposition. For example, the action of the first term in ![]() ,
,
![]() , can be interpreted as projecting the x-component of a vector elastic wavefield onto the P-wave mode, phase shifting it using the P-wave phase velocity and then aligning it with the x-component of the P-wave polarization direction. If individual wave modes are needed to perform imaging, the decoupled operators can be separately applied. The operators concerning a specific wave mode are indicated by the corresponding phase velocity. The first columns in equations 17 and 22 are P-wave propagators, while the second and third columns are
, can be interpreted as projecting the x-component of a vector elastic wavefield onto the P-wave mode, phase shifting it using the P-wave phase velocity and then aligning it with the x-component of the P-wave polarization direction. If individual wave modes are needed to perform imaging, the decoupled operators can be separately applied. The operators concerning a specific wave mode are indicated by the corresponding phase velocity. The first columns in equations 17 and 22 are P-wave propagators, while the second and third columns are ![]() and
and ![]() wave propagators, respectively. In general anisotropic media beyond tilted transverse isotropic (TTI) symmetry, the two S-wave modes do not decouple easily. Therefore, in order to avoid S-wave singularities in wave propagation, the two coupled S-waves should be computed together (Sun et al., 2016a; Cheng et al., 2016).
wave propagators, respectively. In general anisotropic media beyond tilted transverse isotropic (TTI) symmetry, the two S-wave modes do not decouple easily. Therefore, in order to avoid S-wave singularities in wave propagation, the two coupled S-waves should be computed together (Sun et al., 2016a; Cheng et al., 2016).
The proposed framework, however, does not require explicit wave mode decomposition for wave extrapolation. Therefore, it can significantly reduce the computational cost of wave extrapolation, yet still obtain waves free of instability and dispersion artifacts. We also emphasize that the proposed method is capable of handling general anisotropic media, including the case of triclinic anisotropy.
|
|
|
|
Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |