|
|
|
|
Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |
|
|---|
|
ORTw-fd-1,ORTw-ps-1
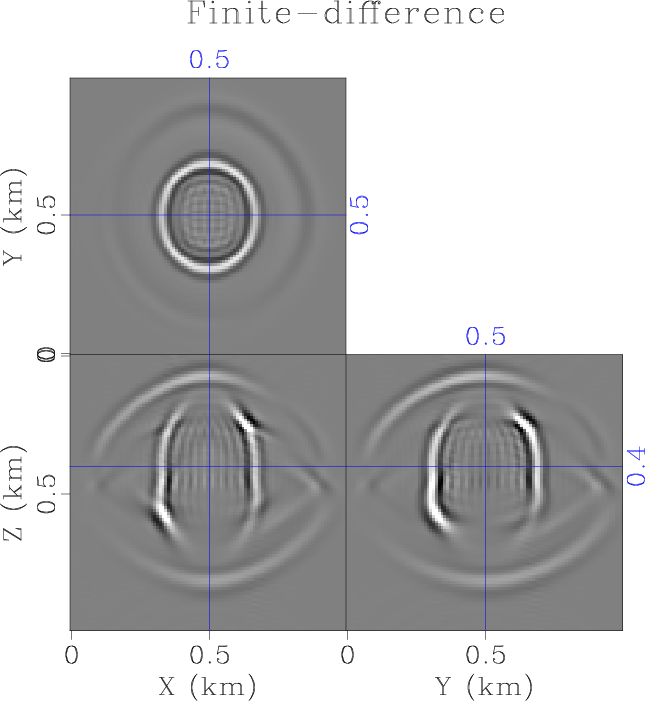
Figure 1. Wavefield snapshot of wavefield propagation in a two-layer orthorhombic model using the finite-difference method (a) and the pseudospectral method (b) with a step size of |
|
|
|
|---|
|
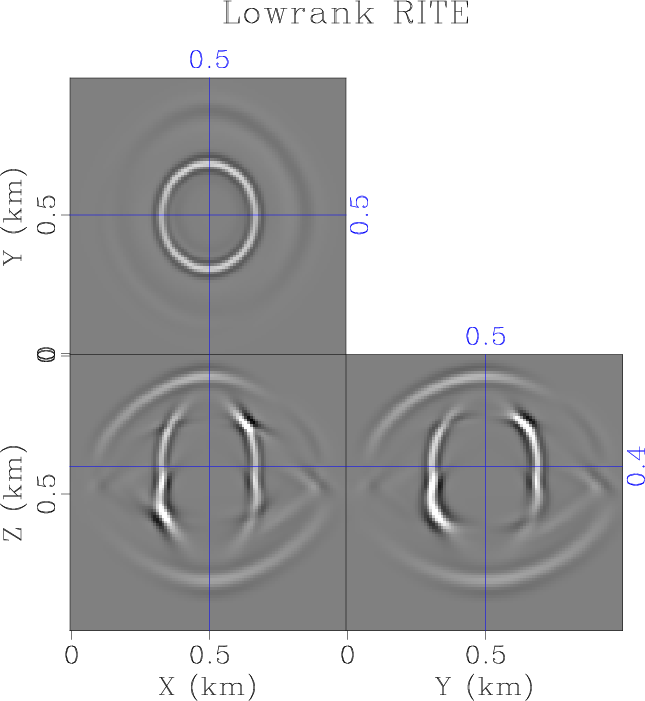
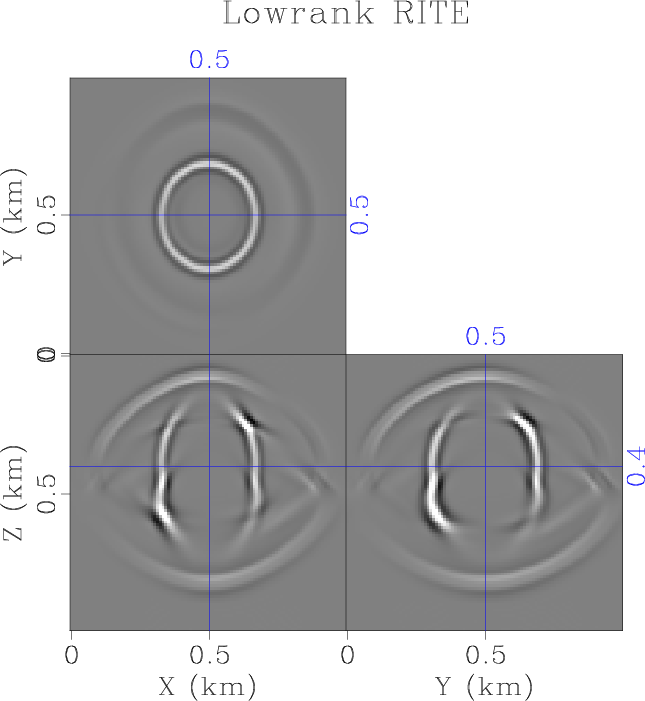
ORTw-lr-1,ORTw-lr-2,ORTw-lr-4,ORTw-lr-8
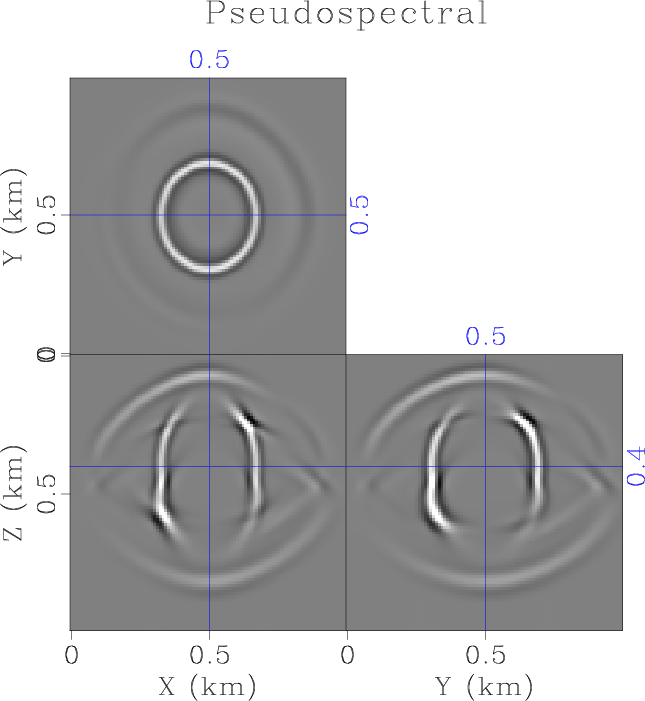
Figure 2. Wavefield snapshot of wavefield propagation in a two-layer orthorhombic model using the proposed low-rank RITE method with a step size of |
|
|
We first test the accuracy and stability of the proposed method in a two-layer orthorhombic model, and compare it with the conventional finite-difference and pseudospectral methods. We construct a two-layer orthorhombic model on a
![]() grid with the density-normalized stiffness tensor (in
grid with the density-normalized stiffness tensor (in ![]() ) of the first layer given in equation 41 (Schoenberg and Helbig, 1997), and the second layer being a scaled version of the first layer by a factor of
) of the first layer given in equation 41 (Schoenberg and Helbig, 1997), and the second layer being a scaled version of the first layer by a factor of ![]() . We apply triangle smoothing in the vertical direction with a radius of
. We apply triangle smoothing in the vertical direction with a radius of ![]() . The spatial sampling rate in all directions of the grid is
. The spatial sampling rate in all directions of the grid is ![]() . A displacement source is oriented at
. A displacement source is oriented at
![]() tilt and
tilt and
![]() azimuth and injected at
azimuth and injected at
![]() . The source wavelet has a peak frequency of
. The source wavelet has a peak frequency of ![]() . A wavefield snapshot shown in Figure 3 was taken at
. A wavefield snapshot shown in Figure 3 was taken at ![]() . The wavefield that was modeled by eighth-order finite-difference in space and second-order finite-difference in time using a time-step size of
. The wavefield that was modeled by eighth-order finite-difference in space and second-order finite-difference in time using a time-step size of ![]() suffers from strong dispersion artifacts (Figure 1a), while the wavefield modeled by pseudospectral method in space and second-order finite-difference in time is free of spatial dispersions. However, increasing the time step size to
suffers from strong dispersion artifacts (Figure 1a), while the wavefield modeled by pseudospectral method in space and second-order finite-difference in time is free of spatial dispersions. However, increasing the time step size to ![]() leads to numerical instability of both methods, and thus the results are not shown. In comparison, the proposed low-rank RITE method shows an accurate result free from dispersion and instability using increasing time step sizes of
leads to numerical instability of both methods, and thus the results are not shown. In comparison, the proposed low-rank RITE method shows an accurate result free from dispersion and instability using increasing time step sizes of ![]() ,
, ![]() ,
, ![]() and
and ![]() (Figure 3).
(Figure 3).
|
|---|
|
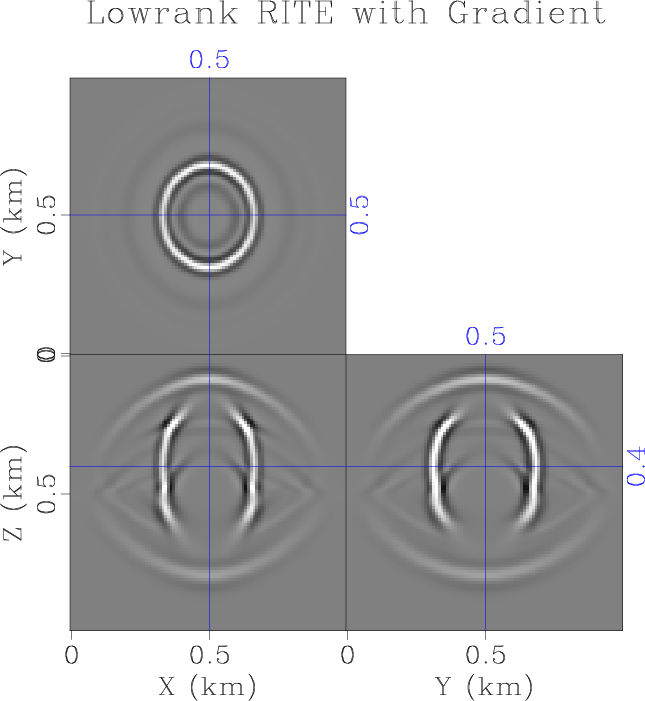
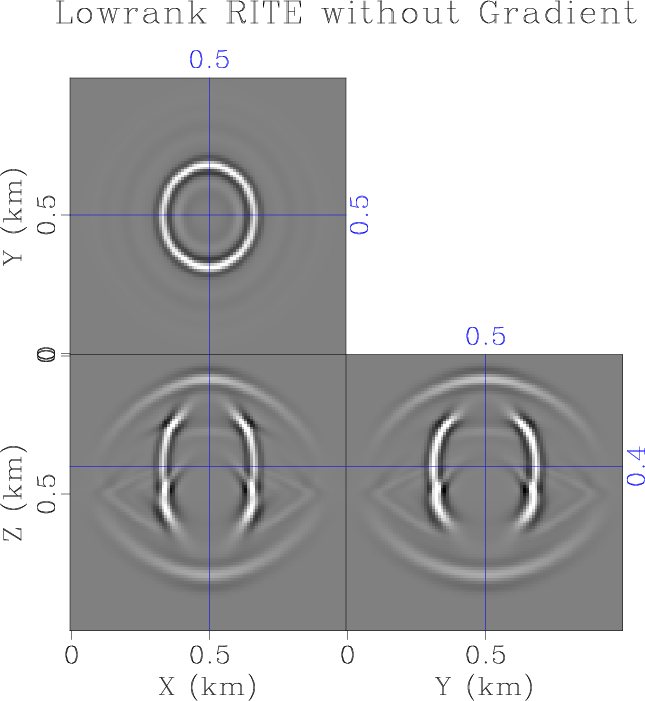
ORTw-lr-1,ORTw-lr0-1
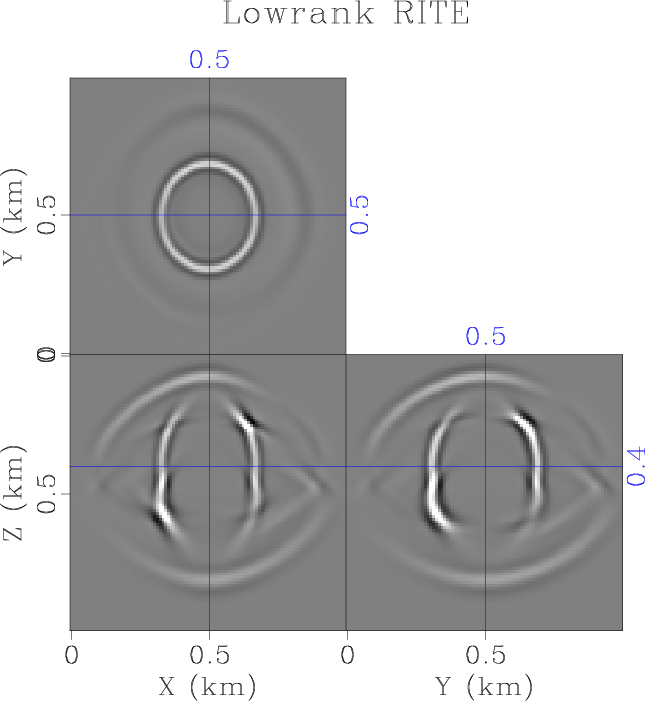
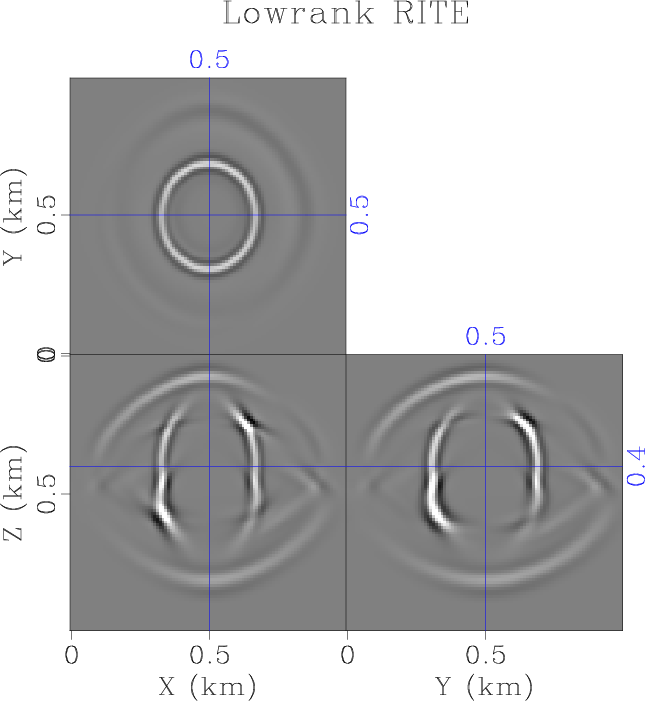
Figure 3. Wavefield snapshot of wavefield propagation in a two-layer orthorhombic model using the low-rank RITE method with (a) and without (b) accounting for the gradient of stiffnesses. |
|
|

|
|---|
|
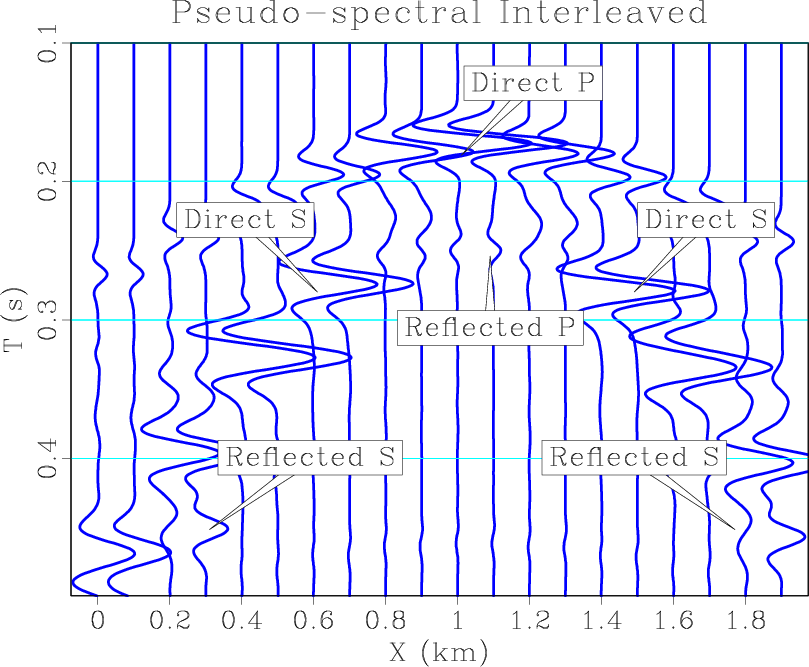
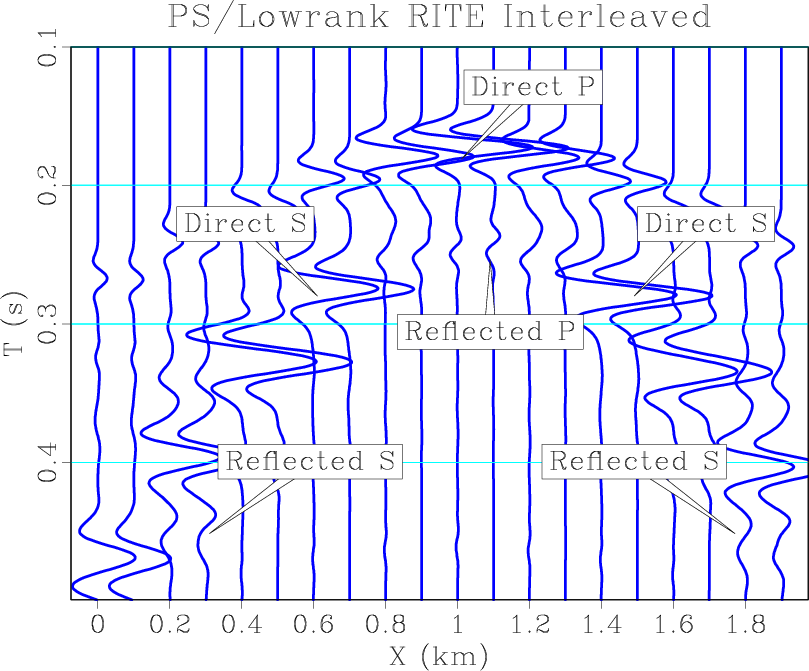
inter-lr,inter-ps,inter-pslr
Figure 4. Interleaved shot gathers extracted at |
|
|
Next, to test wave extrapolation accuracy at a medium interface, where strong heterogeneity occurs, we use the same two-layer orthorhombic model without smoothing in the vertical direction. Figure 3 shows wavefield snapshots taken at ![]() . Because of the strong contrast at the medium interface, the transmitted and reflected waves calculated by the proposed method including the stiffness gradient terms demonstrates noticeable amplitude and phase differences compared with the waves calculated by ignoring the gradient terms. Figure 4a shows interleaved shot gathers extracted at
. Because of the strong contrast at the medium interface, the transmitted and reflected waves calculated by the proposed method including the stiffness gradient terms demonstrates noticeable amplitude and phase differences compared with the waves calculated by ignoring the gradient terms. Figure 4a shows interleaved shot gathers extracted at ![]() , which compares the modeled data by the low-rank method and the pseudo-spectral method, both with and without accounting for the stiffness gradient terms. We can observe that for either the low-rank or the pseudo-spectral methods, modeled direct P- and S-arrivals are identical while reflected P- and S-arrivals show obvious difference in both amplitude and phase due to the missing of stiffness gradient terms. To validate our observation, we also carry out wave extrapolation using the pseudo-spectral method by solving first- and second-order elastic wave equations. Their shot gather, shown in Figure 4b, demonstrates the same phenomena. Finally, in Figure 4c, we interleave the amplitude-normalized shot gathers from low-rank RITE solution including the stiffness gradients, togethr with a pseudo-spectral solution of the first-order equations. They demonstrate almost identical amplitude and phase behavior. In terms of computational cost, the numerical ranks of the wave extrapolation matrices are
, which compares the modeled data by the low-rank method and the pseudo-spectral method, both with and without accounting for the stiffness gradient terms. We can observe that for either the low-rank or the pseudo-spectral methods, modeled direct P- and S-arrivals are identical while reflected P- and S-arrivals show obvious difference in both amplitude and phase due to the missing of stiffness gradient terms. To validate our observation, we also carry out wave extrapolation using the pseudo-spectral method by solving first- and second-order elastic wave equations. Their shot gather, shown in Figure 4b, demonstrates the same phenomena. Finally, in Figure 4c, we interleave the amplitude-normalized shot gathers from low-rank RITE solution including the stiffness gradients, togethr with a pseudo-spectral solution of the first-order equations. They demonstrate almost identical amplitude and phase behavior. In terms of computational cost, the numerical ranks of the wave extrapolation matrices are ![]() when the stiffness gradient terms are not included, while the ranks increase to
when the stiffness gradient terms are not included, while the ranks increase to ![]() when the gradient terms are included.
when the gradient terms are included.
|
|---|
|
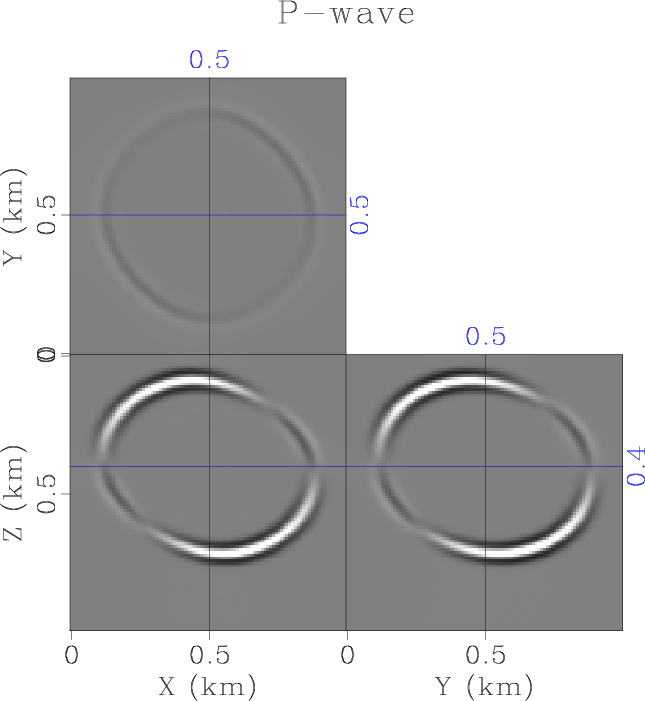
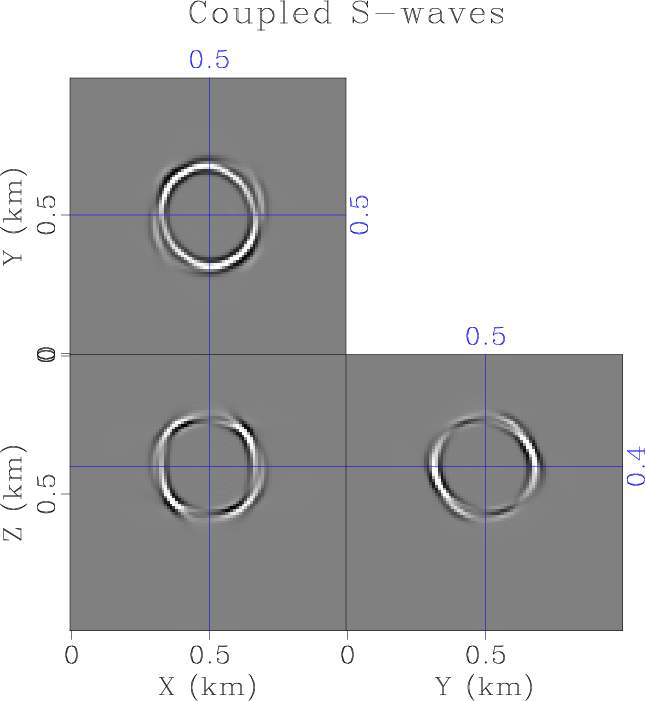
TRIw-lr-p,TRIw-lr-s
Figure 5. Wavefield snapshot of (a) P-wave and (b) coupled S-waves propagation in a perturbed triclinic model using the proposed low-rank RITE method with a step size of |
|
|
In the third example, we test the ability of the proposed method to model decomposed wave mode propagation in a more general anisotropic medium, a triclinic medium. We use the lab measurements from Mah and Schmitt (2003) as the background model, with the stiffness tensors (in GPa) of the triclinic model shown in equation 42, which is then normalized by a mass density of
![]() . We then add spherical perturbations centered at
. We then add spherical perturbations centered at
![]() to all the density normalized stiffness tensors to make the models mildly heterogeneous. Using the same mesh size as the previous example, and a time step size of
to all the density normalized stiffness tensors to make the models mildly heterogeneous. Using the same mesh size as the previous example, and a time step size of ![]() , the proposed method is capable of accurately and separately propagating P- and S-waves in the triclinic medium (Figure 5) using equation 16. The two S-wave modes are propagated together since they do not decouple easily. Both the P- and coupled S-waves are free of numerical dispersion and instablity. The numercial ranks of the wave extrapolation matrices for this test are
, the proposed method is capable of accurately and separately propagating P- and S-waves in the triclinic medium (Figure 5) using equation 16. The two S-wave modes are propagated together since they do not decouple easily. Both the P- and coupled S-waves are free of numerical dispersion and instablity. The numercial ranks of the wave extrapolation matrices for this test are ![]() .
.
|
|---|
|
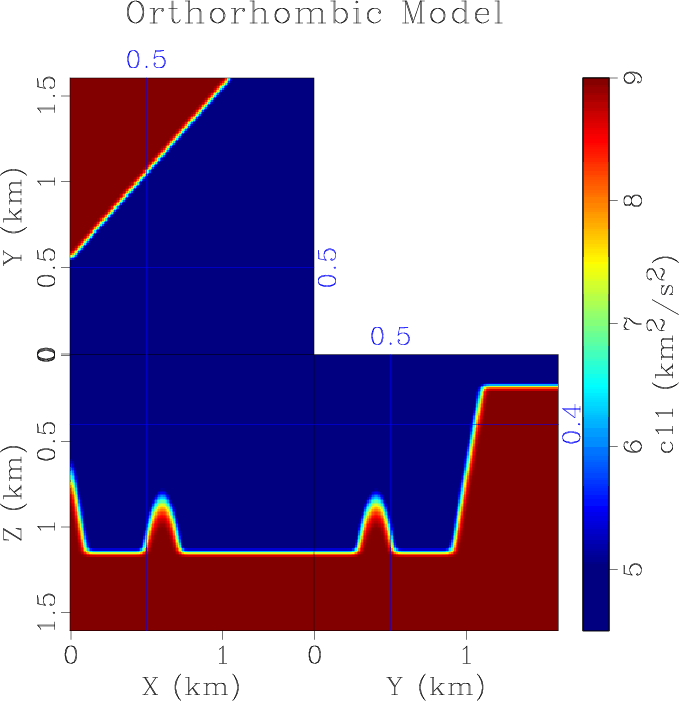
ORTc-11-f
Figure 6. (a) |
|
|
|
|---|
|
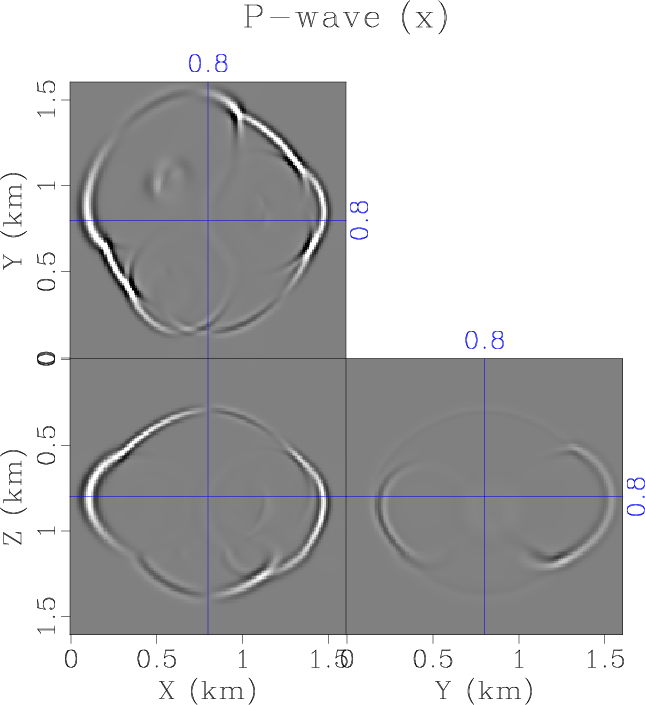
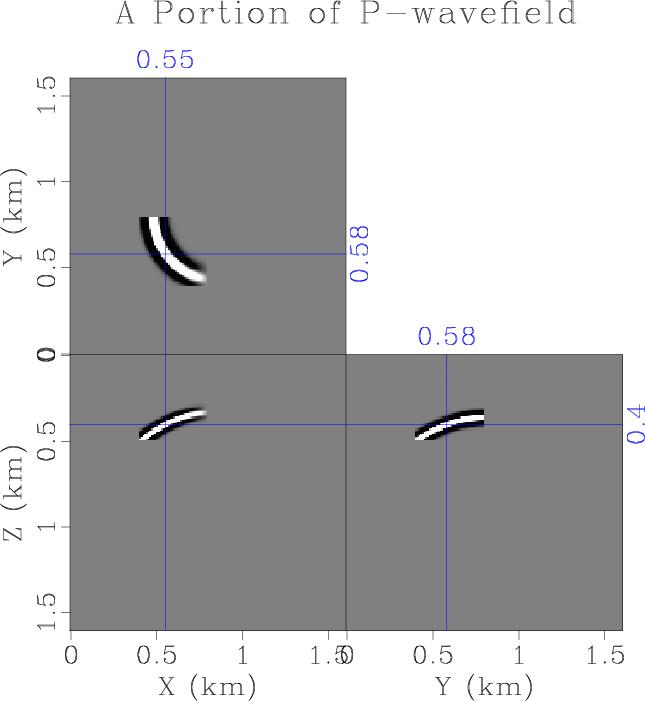
ORTw-lr-p-x,snap-p-x-cut
Figure 7. (a) The x-component of decoupled P-wavefield at |
|
|

|
|---|
|
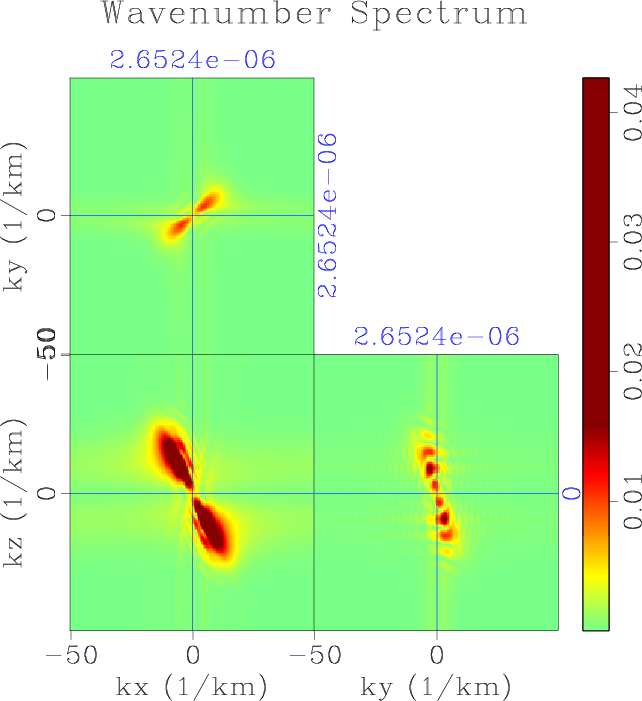
freq-p-x,freq-p-x2
Figure 8. Wavenumber amplitude spectrum of (a) the analytical wavefield, and (b) its real part. |
|
|
|
|---|
|
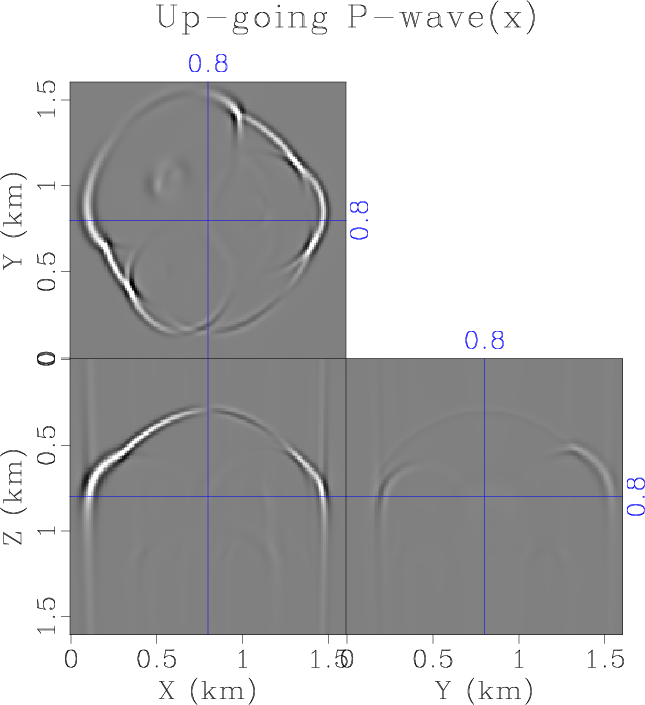
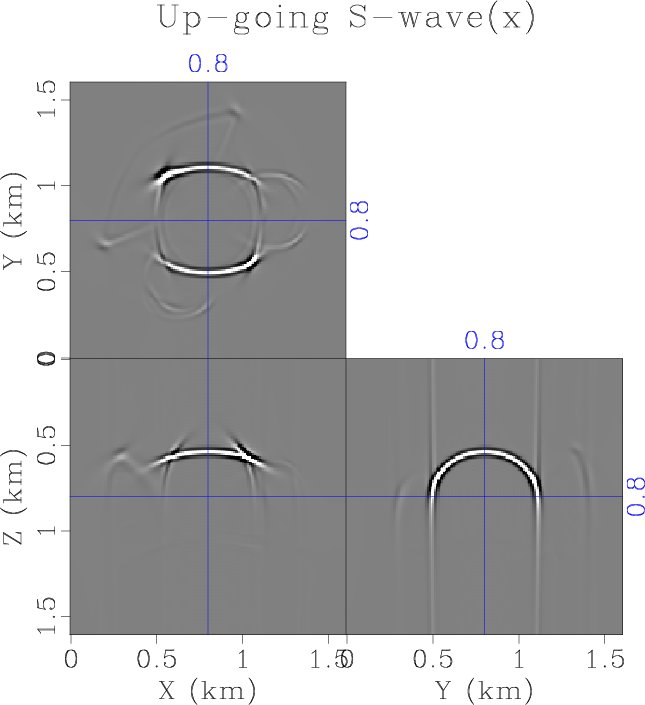
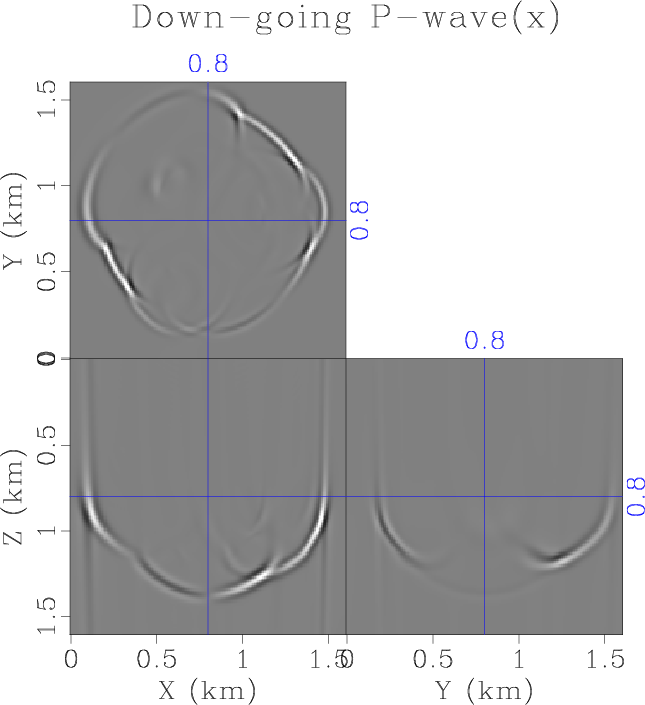
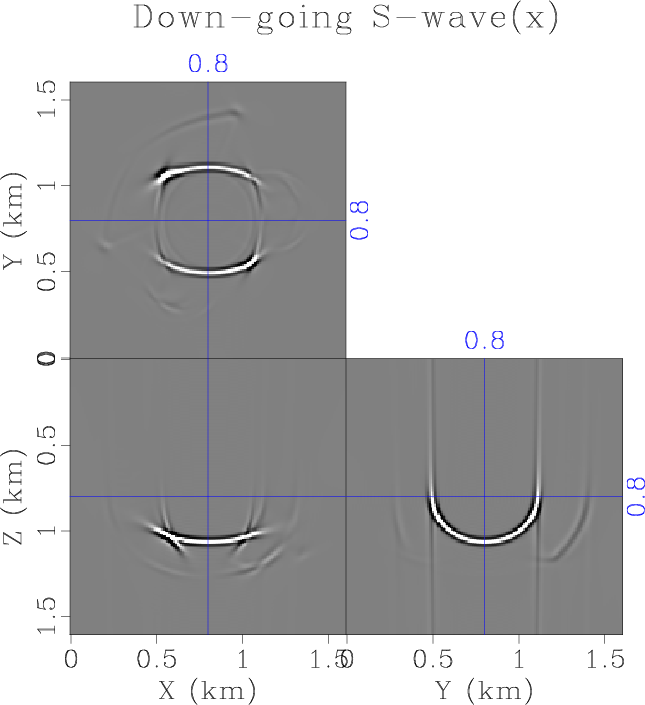
snap-p-x-up,snap-s-x-up,snap-p-x-dn,snap-s-x-dn
Figure 9. The decomposition of wavefield into up- and down-going directions. (a) The up-going P-wave, and (b) the up-going S-wave. (c) The down-going P-wave. (d) The down-going S-wave. |
|
|
In the last example, we demonstrate one advantage of the proposed method for seismic imaging applications, the accessibility of directional information of wavefield. For a real-valued wavefield, the propagation direction cannot be uniquely defined in the wavenumber domain because of its symmetric wavenumber spectrum about zero (Hu et al., 2016). This is due to the fact that the real-valued wavefield contains both positive and negative frequency components. The analytical wavefield, on the other hand, has decoupled positive and negative frequency components, so its wavenumber spectrum reveals the direction of wavefield propagation. To demonstrate this fact, we construct an orthorhombic model based on the French model (French, 1974), with its ![]() component shown in Figure 6. We use equation 16 to calculate a decoupled P-wavefield, whose x-component at
component shown in Figure 6. We use equation 16 to calculate a decoupled P-wavefield, whose x-component at ![]() is shown in Figure 7a. We select a portion of the wavefield centered at
is shown in Figure 7a. We select a portion of the wavefield centered at
![]() propagating in the direction negative along all three axes, as shown in Figure 7b. Figure 8a shows the wavenumber amplitude spectrum of the wavefield, and its energy are all distributed in the positive octant. One the other hand, the wavenumber amplitude spectrum of the real part of the wavefield shows symmetric distribution of energy about the origin, as demonstrated by Figure 8b. Finally, we decouple the upward-traveling and downward-traveling wavefield based on the sign
propagating in the direction negative along all three axes, as shown in Figure 7b. Figure 8a shows the wavenumber amplitude spectrum of the wavefield, and its energy are all distributed in the positive octant. One the other hand, the wavenumber amplitude spectrum of the real part of the wavefield shows symmetric distribution of energy about the origin, as demonstrated by Figure 8b. Finally, we decouple the upward-traveling and downward-traveling wavefield based on the sign ![]() , and the downward-traveling P- and S-waves are shown in Figure 9c and 9d.
, and the downward-traveling P- and S-waves are shown in Figure 9c and 9d.
|
|
|
|
Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |