 |
 |
 |
 | Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |  |
![[pdf]](icons/pdf.png) |
Next: Energy-norm imaging condition
Up: Theory
Previous: Heterogeneous media
So far, we have laid out our basic theory of recursive integral time extrapolation of elastic waves. In mildly heterogeneous media, the Christoffel matrix is SPD. In strongly heterogeneous media, the Christoffel matrix becomes complex-valued and non-Hermitian. However, in both cases, the eigenvalues and eigenvectors of the Christoffel matrix become dependent on both spatial location and propagation direction, in other words, they are functions of both space
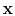 and wavenumber
and wavenumber
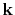 . If these operators are implemented straightforwardly, one is faced with the daunting task of computing and storing the complete eigenvalue decomposition of the Christoffel matrix using all the combinations of
. If these operators are implemented straightforwardly, one is faced with the daunting task of computing and storing the complete eigenvalue decomposition of the Christoffel matrix using all the combinations of
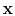 and
and
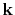 , leading to
, leading to
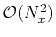 computational and memory complexity, where
computational and memory complexity, where  refers to the total number of mesh points in
refers to the total number of mesh points in 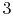 D. To perform wave extrapolation in the form of integral operators, one would have to multiply matrices with vectors in dimension of
D. To perform wave extrapolation in the form of integral operators, one would have to multiply matrices with vectors in dimension of  , leading to a computational complexity of
, leading to a computational complexity of
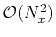 . This is simply infeasible for practical applications.
. This is simply infeasible for practical applications.
In this work, to efficiently apply the derived Fourier Integral Operators (FIOs), we proposed to apply the low-rank decomposition (Fomel et al., 2013) on the mixed-domain wave extrapolation matrices. Take the wave extrapolation operator in equation 27,
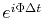 , as an example. We propose to apply low-rank approximation on each individual element of its expansion. For instance, the
, as an example. We propose to apply low-rank approximation on each individual element of its expansion. For instance, the
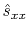 element, which operates on the x-component of the input vector wavefield and outputs to the x-component of the output vector wavefield, can be approximated as (Fomel et al., 2013):
element, which operates on the x-component of the input vector wavefield and outputs to the x-component of the output vector wavefield, can be approximated as (Fomel et al., 2013):
 |
(29) |
where
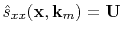 and
and
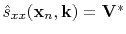 are sampled representative columns and rows from the original matrix
are sampled representative columns and rows from the original matrix
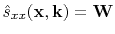 ,
, 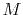 and
and 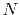 are the numerical ranks of matrix
are the numerical ranks of matrix
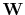 , and the matrix
, and the matrix
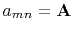 is obtained from minimizing
is obtained from minimizing
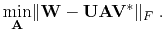 |
(30) |
Similarly,
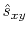 and
and
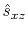 can be approximated as:
can be approximated as:
The computation of
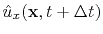 then becomes:
then becomes:
The computation of 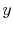 and
and 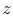 components can be carried out in a similar fashion. The computational cost of applying each FIO reduces to a complexity of
components can be carried out in a similar fashion. The computational cost of applying each FIO reduces to a complexity of
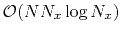 , where
, where
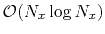 is the complexity of one forward or inverse Fast Fourier Transform (FFT), and
is the complexity of one forward or inverse Fast Fourier Transform (FFT), and 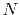 is the numerical rank of the low-rank approximation, which is
is the numerical rank of the low-rank approximation, which is  for homogeneous media and
for homogeneous media and
 for heterogeneous media.
for heterogeneous media.
 |
 |
 |
 | Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |  |
![[pdf]](icons/pdf.png) |
Next: Energy-norm imaging condition
Up: Theory
Previous: Heterogeneous media
2018-11-16
![]() , as an example. We propose to apply low-rank approximation on each individual element of its expansion. For instance, the
, as an example. We propose to apply low-rank approximation on each individual element of its expansion. For instance, the
![]() element, which operates on the x-component of the input vector wavefield and outputs to the x-component of the output vector wavefield, can be approximated as (Fomel et al., 2013):
element, which operates on the x-component of the input vector wavefield and outputs to the x-component of the output vector wavefield, can be approximated as (Fomel et al., 2013):