|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: Numerical examples Up: Sripanich et al.: Effects Previous: Layer traveltime derivatives with
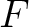 ,
, 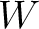 , and their derivatives in all sublayers, we compute the layer traveltime derivatives (equation 15) for a specified CMP location in the case of reflection traveltime or a specified image-ray escape location in the case of diffraction traveltime. In particular, equation 15 can be rewritten with evaluated reference 1-D traveltime derivatives as follows:
, and their derivatives in all sublayers, we compute the layer traveltime derivatives (equation 15) for a specified CMP location in the case of reflection traveltime or a specified image-ray escape location in the case of diffraction traveltime. In particular, equation 15 can be rewritten with evaluated reference 1-D traveltime derivatives as follows:
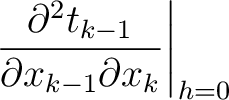 |
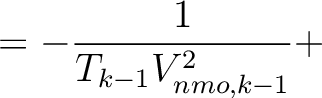 H H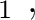 |
(18) |
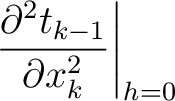 |
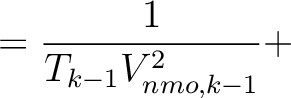 H H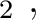 |
|
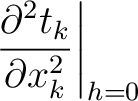 |
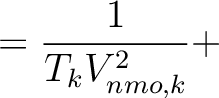 H H |
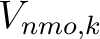 is the NMO velocity of the
is the NMO velocity of the 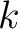 -th layer at the specified position. This velocity is constant for an isotropic sublayer but is equal to
-th layer at the specified position. This velocity is constant for an isotropic sublayer but is equal to
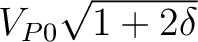 for a VTI sublayer, where
for a VTI sublayer, where 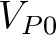 is the vertical P-wave velocity and
is the vertical P-wave velocity and 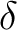 is the Thomsen's delta.
is the Thomsen's delta.
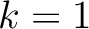 with
with 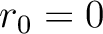 and end up with
and end up with
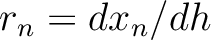 .
.
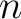 -th layer and
-th layer and 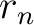 from step 2.
from step 2.
 .
.