|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: Numerical implementation Up: Sripanich et al.: Effects Previous: Laterally varying velocity
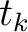 that includes the heterogeneity effects. Twice differentiating the result with respect to
that includes the heterogeneity effects. Twice differentiating the result with respect to 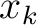 and
and 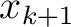 and evaluating at the vertical reference (
and evaluating at the vertical reference (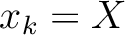 and
and 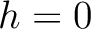 ), we arrive at the following layer traveltime derivatives:
), we arrive at the following layer traveltime derivatives:
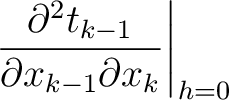 |
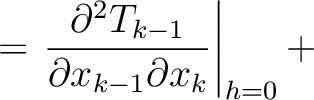 H H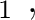 |
(15) |
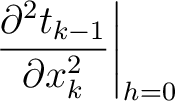 |
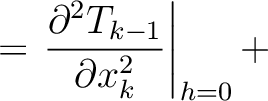 H H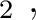 |
|
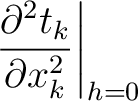 |
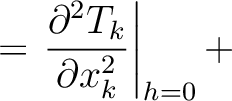 H H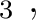 |
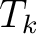 denotes the traveltime of the
denotes the traveltime of the 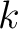 -th layer in the reference 1-D horizontally-layered anisotropic media with constant elastic parameters within each layer. Therefore, the terms with
-th layer in the reference 1-D horizontally-layered anisotropic media with constant elastic parameters within each layer. Therefore, the terms with 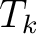 derivatives are the usual results ones get under the 1-D medium assumption. The additional heterogeneous terms (H
derivatives are the usual results ones get under the 1-D medium assumption. The additional heterogeneous terms (H ) that combine the effects from curved interfaces and laterally varying velocity are given by
) that combine the effects from curved interfaces and laterally varying velocity are given by
H |
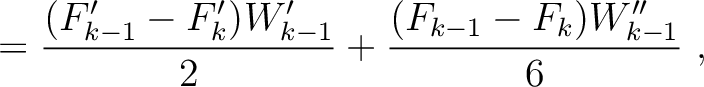 |
(16) |
H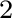 |
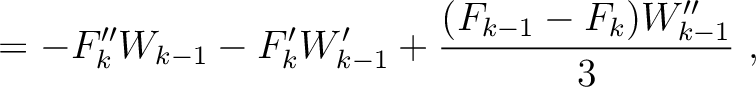 |
|
H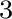 |
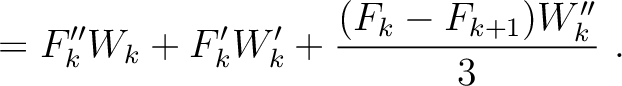 |
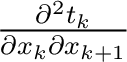 is similar to that of
is similar to that of
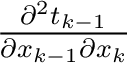 with shifted indices. If a single horizontal layer is considered, equation 11 becomes reminiscent of the result by Grechka and Tsvankin (1999):
but with the second derivative on group slowness as opposed to group velocity.
with shifted indices. If a single horizontal layer is considered, equation 11 becomes reminiscent of the result by Grechka and Tsvankin (1999):
but with the second derivative on group slowness as opposed to group velocity. 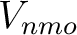 is the usual normal-moveout velocity in the reference 1-D medium, which translates to
is the usual normal-moveout velocity in the reference 1-D medium, which translates to 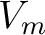 in the case of diffraction traveltime.
in the case of diffraction traveltime.