|
|
|
|
Theory of differential offset continuation |
Equation (104) has the known general solution,
expressed in terms of cylinder functions of complex order
![]() (Watson, 1952)
(Watson, 1952)
In the general case of offset continuation, ![]() and
and ![]() are
constrained by the two initial conditions (62) and
(63). In the special case of continuation from zero offset, we
can neglect the second term in (106) as vanishing at the zero
offset. The remaining term defines the following operator of inverse
DMO in the
are
constrained by the two initial conditions (62) and
(63). In the special case of continuation from zero offset, we
can neglect the second term in (106) as vanishing at the zero
offset. The remaining term defines the following operator of inverse
DMO in the ![]() domain:
domain:
The DMO operator now can be derived as the inversion of operator
(107), which is a simple multiplication by
![]() . Therefore, offset continuation becomes a
multiplication by
. Therefore, offset continuation becomes a
multiplication by
![]() (the cascade
of two operators). This fact demonstrates an important advantage of
moving to the log-stretch domain: both offset continuation and DMO are simple
filter multiplications in the Fourier domain of the log-stretched time
coordinate.
(the cascade
of two operators). This fact demonstrates an important advantage of
moving to the log-stretch domain: both offset continuation and DMO are simple
filter multiplications in the Fourier domain of the log-stretched time
coordinate.
In order to compare operator (107) with the known versions
of log-stretch DMO, we need to derive its asymptotic representation
for high frequency ![]() . The required asymptotic expression
follows directly from the definition of function
. The required asymptotic expression
follows directly from the definition of function ![]() in
equation (108) and the known asymptotic representation for a Bessel
function of high order (Watson, 1952):
in
equation (108) and the known asymptotic representation for a Bessel
function of high order (Watson, 1952):
The asymptotic representation (110) is valid for high
frequency ![]() and
and
![]() . The
phase function
. The
phase function ![]() defined in (112) coincides precisely
with the analogous term in Liner's exact log DMO
(Liner, 1990), which provides the correct
geometric properties of DMO. Similar expressions for the log-stretch
phase factor
defined in (112) coincides precisely
with the analogous term in Liner's exact log DMO
(Liner, 1990), which provides the correct
geometric properties of DMO. Similar expressions for the log-stretch
phase factor ![]() were derived in different ways by
Zhou et al. (1996) and Canning and Gardner (1996).
However, the amplitude term
were derived in different ways by
Zhou et al. (1996) and Canning and Gardner (1996).
However, the amplitude term ![]() differs from the previously
published ones because of the difference in the amplitude preservation
properties.
differs from the previously
published ones because of the difference in the amplitude preservation
properties.
A number of approximate log DMO operators have been proposed in the
literature. As shown by Liner (1990), all of them but
exact log DMO distort the geometry of reflection effects at large
offsets. The distortion is caused by the implied approximations of the
true phase function ![]() . Bolondi's OC operator
(Bolondi et al., 1982) implies
. Bolondi's OC operator
(Bolondi et al., 1982) implies
![]() , Notfors' DMO (Notfors and Godfrey, 1987) implies
, Notfors' DMO (Notfors and Godfrey, 1987) implies
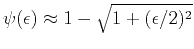 , and the ``full
DMO'' (Bale and Jakubowicz, 1987) has
, and the ``full
DMO'' (Bale and Jakubowicz, 1987) has
![]() . All these approximations are
valid for small
. All these approximations are
valid for small ![]() (small offsets or small reflector dips) and
have errors of the order of
(small offsets or small reflector dips) and
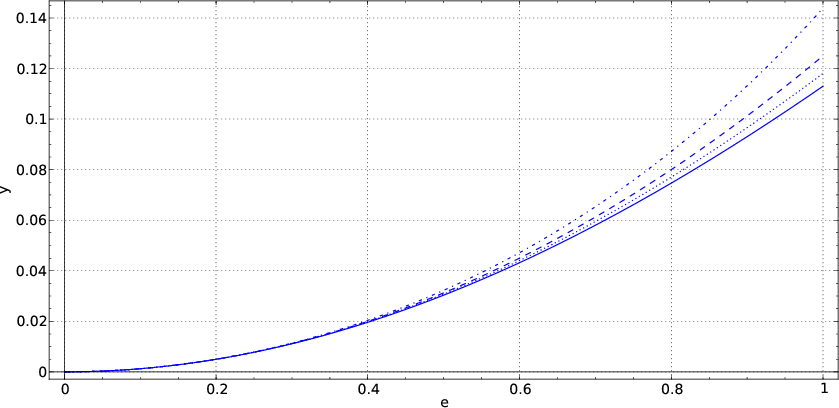
have errors of the order of ![]() (Figure 6). The
range of validity of Bolondi's operator is defined in
equation (22).
(Figure 6). The
range of validity of Bolondi's operator is defined in
equation (22).
|
pha
Figure 6. Phase functions of the log DMO operators. Solid line: exact log DMO; dashed line: Bolondi's OC; dashed-dotted line: Bale's full DMO; dotted line: Notfors' DMO. |
|
|---|---|
|
|
In practice, seismic data are often irregularly sampled in space but
regularly sampled in time. This makes it attractive to apply offset
continuation and DMO operators in the ![]() domain, where
the frequency
domain, where
the frequency ![]() corresponds to the log-stretched time and
corresponds to the log-stretched time and
![]() is the midpoint coordinate. Performing the inverse Fourier
transform on the spatial frequency transforms the inverse DMO
operator (107) to the
is the midpoint coordinate. Performing the inverse Fourier
transform on the spatial frequency transforms the inverse DMO
operator (107) to the ![]() domain, where the
filter multiplication becomes a convolutional operator:
domain, where the
filter multiplication becomes a convolutional operator:
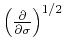 , which,
in turn, is equal to the
, which,
in turn, is equal to the
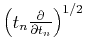 term of the asymptotic OC
operator (69). The difference between the exact
filter
term of the asymptotic OC
operator (69). The difference between the exact
filter
|
|---|
|
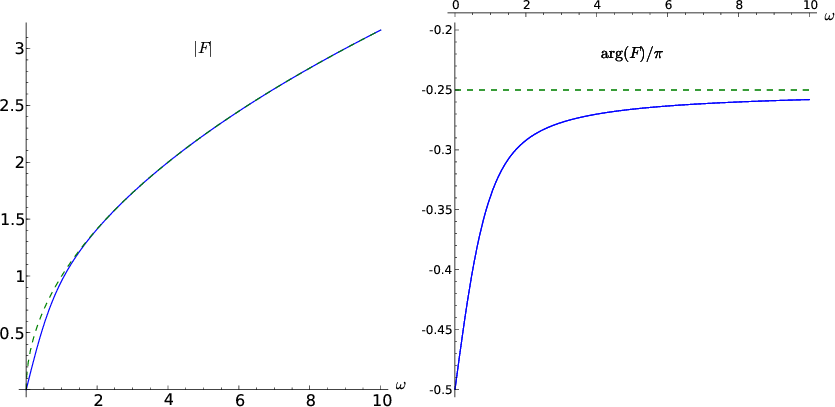
flt
Figure 7. Amplitude (left) and phase (right) of the time filter in the log-stretch domain. The solid line is for the exact filter; the dashed line for its approximation by the half-order derivative filter. The horizontal axis corresponds to the dimensionless log-stretch frequency |
|
|
Inverting operator (113), we can obtain the DMO operator in the
![]() domain.
domain.
|
|
|
|
Theory of differential offset continuation |