|
|
|
|
Theory of differential offset continuation |
Given a post-NMO constant-offset section at half-offset ![]()
Equation (1) belongs to the hyperbolic type, with
the offset coordinate ![]() being a ``time-like'' variable and the
midpoint coordinate
being a ``time-like'' variable and the
midpoint coordinate ![]() and the time
and the time ![]() being ``space-like''
variables. The last condition (63) is required for the
initial value problem to be well-posed (Courant, 1962). From a physical
point of view, its role is to separate the two different wave-like
processes embedded in equation (1), which are
analogous to inward and outward wave propagation. We will associate
the first process with continuation to a larger offset and the second
one with continuation to a smaller offset. Though the offset
derivatives of data are not measured in practice, they can be
estimated from the data at neighboring offsets by a finite-difference
approximation. Selecting a propagation branch explicitly, for example
by considering the high-frequency asymptotics of the continuation
operators, can allow us to eliminate the need for
condition (63). In this section, I discuss the exact
integral solution of the OC equation and analyze its asymptotics.
being ``space-like''
variables. The last condition (63) is required for the
initial value problem to be well-posed (Courant, 1962). From a physical
point of view, its role is to separate the two different wave-like
processes embedded in equation (1), which are
analogous to inward and outward wave propagation. We will associate
the first process with continuation to a larger offset and the second
one with continuation to a smaller offset. Though the offset
derivatives of data are not measured in practice, they can be
estimated from the data at neighboring offsets by a finite-difference
approximation. Selecting a propagation branch explicitly, for example
by considering the high-frequency asymptotics of the continuation
operators, can allow us to eliminate the need for
condition (63). In this section, I discuss the exact
integral solution of the OC equation and analyze its asymptotics.
The integral solution of problem (62-63)
for equation (1) is obtained in with the help of
the classic methods of mathematical physics
(Fomel, 2001,1994). It takes the explicit form
From equations (65) and (66) one can see
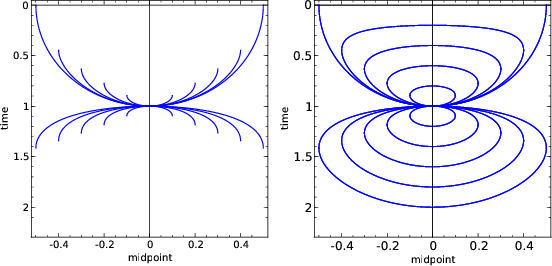
that the impulse response of the offset continuation operator is
discontinuous in the time-offset-midpoint space on a surface defined
by the equality
|
|---|
|
cont
Figure 5. Constant-offset sections of the characteristic conoid - ``offset continuation fronts'' (left), and branches of the conoid used in the integral OC operator (right). The upper part of the plots (small times) corresponds to continuation to smaller offsets; the lower part (large times) corresponds to larger offsets. |
|
|
As a second-order differential equation of the hyperbolic type,
equation (1) describes two different processes. The
first process is ``forward'' continuation from smaller to larger
offsets, the second one is ``reverse'' continuation in the opposite
direction. These two processes are clearly separated in the
high-frequency asymptotics of operator (64). To obtain
the asymptotic representation, it is sufficient to note that
![]() is the impulse response
of the causal half-order integration operator and that
is the impulse response
of the causal half-order integration operator and that
![]() is asymptotically equivalent to
is asymptotically equivalent to
![]()
![]() . Thus, the asymptotical form of
the integral offset-continuation operator becomes
. Thus, the asymptotical form of
the integral offset-continuation operator becomes
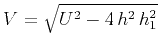 ;
;
In the high-frequency asymptotics, it is possible to replace the two
terms in equation (69) with a single term
(Fomel, 2003a). The single-term expression is
| (73) |
The limit of expression (70) for the output offset ![]() approaching zero can be evaluated by L'Hospitale's rule. As one would
expect, it coincides with the well-known expression for the summation
path of the integral DMO operator
(Deregowski and Rocca, 1981)
approaching zero can be evaluated by L'Hospitale's rule. As one would
expect, it coincides with the well-known expression for the summation
path of the integral DMO operator
(Deregowski and Rocca, 1981)
|
|
|
|
Theory of differential offset continuation |