 |
 |
 |
 | Theory of differential offset continuation |  |
![[pdf]](icons/pdf.png) |
Next: Integral offset continuation operator
Up: Introducing the offset continuation
Previous: Example 3: elliptic reflector
Let us now consider the connection between the laws of traveltime
transformation and the laws of the corresponding amplitude
transformation. The change of the wave amplitudes in the OC process
is described by the first-order partial differential transport
equation (5). We can find the general solution of
this equation by applying the method of characteristics. The solution
takes the explicit integral form
![\begin{displaymath}
A_n\left(t_n\right)=A_0\left(t_0\right)\,\exp{\left(\int_{t_...
...u_n \over \partial h} \right)^{-1}\right]\,
d\tau_n\right)}\;.
\end{displaymath}](img119.png) |
(42) |
The integral in equation (42) is defined on a curved
time ray, and 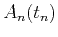 stands for the amplitude transported along
this ray. In the case of a plane dipping reflector, the ray amplitude
can be immediately evaluated by substituting the explicit traveltime
and time ray equations from the preceding section
into (42). The amplitude expression in this case takes
the simple form
stands for the amplitude transported along
this ray. In the case of a plane dipping reflector, the ray amplitude
can be immediately evaluated by substituting the explicit traveltime
and time ray equations from the preceding section
into (42). The amplitude expression in this case takes
the simple form
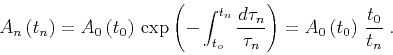 |
(43) |
In order to consider the more general case of a curvilinear reflector,
we need to take into account the connection between the traveltime
derivatives in (42) and the geometry of the reflector.
As follows directly from the trigonometry of the incident and
reflected rays triangle (Figure 1),
where 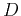 is the length of the normal ray. Let
is the length of the normal ray. Let  be the
zero-offset reflection traveltime. Combining
equations (44) and (46) with
(9), we can get the following relationship:
be the
zero-offset reflection traveltime. Combining
equations (44) and (46) with
(9), we can get the following relationship:
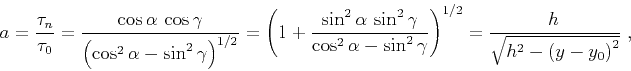 |
(47) |
which describes the ``DMO smile'' (40) found by
Deregowski and Rocca (1981) in geometric terms.
Equation (47) allows for a convenient change of variables
in equation (42). Let the reflection angle 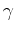 be a
parameter monotonically increasing along a time ray. In this case,
each time ray is uniquely determined by the position of the reflection
point, which in turn is defined by the values of
be a
parameter monotonically increasing along a time ray. In this case,
each time ray is uniquely determined by the position of the reflection
point, which in turn is defined by the values of 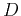 and
and 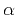 .
According to this change of variables, we can
differentiate (47) along a time ray to get
.
According to this change of variables, we can
differentiate (47) along a time ray to get
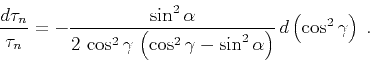 |
(48) |
Note also that the quantity
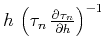 in equation (42) coincides
exactly with the time ray invariant
in equation (42) coincides
exactly with the time ray invariant 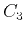 found in
equation (27). Therefore its value is constant along each
time ray and equals
found in
equation (27). Therefore its value is constant along each
time ray and equals
 |
(49) |
Finally, as shown in Appendix ![[*]](icons/crossref.png) ,
,
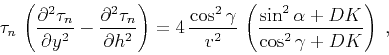 |
(50) |
where 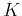 is the reflector curvature at the reflection point.
Substituting (48), (49), and (50)
into (42) transforms the integral to the form
is the reflector curvature at the reflection point.
Substituting (48), (49), and (50)
into (42) transforms the integral to the form
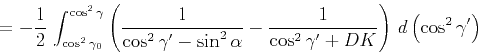 |
(51) |
which we can evaluate analytically. The final equation for the
amplitude transformation is
In case of a plane reflector, the curvature 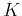 is zero, and
equation (52) coincides with (43).
In the general case can be rewritten as
is zero, and
equation (52) coincides with (43).
In the general case can be rewritten as
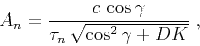 |
(53) |
where 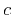 is constant along each time ray (it may vary with the reflection point
location on the reflector but not with the offset). We should compare equation
(53)
with the known expression for the reflection wave amplitude of the leading
ray series term in 2.5-D media (Bleistein et al., 2001):
is constant along each time ray (it may vary with the reflection point
location on the reflector but not with the offset). We should compare equation
(53)
with the known expression for the reflection wave amplitude of the leading
ray series term in 2.5-D media (Bleistein et al., 2001):
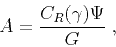 |
(54) |
where 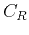 stands for the angle-dependent reflection coefficient,
stands for the angle-dependent reflection coefficient, 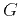 is the
geometric spreading
is the
geometric spreading
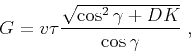 |
(55) |
and 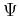 includes other possible factors (such as the source
directivity) that we can either correct or neglect in the preliminary
processing. It is evident that the curvature dependence of the
amplitude transformation (53) coincides completely with
the true geometric spreading factor (55) and that the angle
dependence of the reflection coefficient is not accounted for the offset
continuation process. If the wavelet shape of the reflected wave on
seismic sections [
includes other possible factors (such as the source
directivity) that we can either correct or neglect in the preliminary
processing. It is evident that the curvature dependence of the
amplitude transformation (53) coincides completely with
the true geometric spreading factor (55) and that the angle
dependence of the reflection coefficient is not accounted for the offset
continuation process. If the wavelet shape of the reflected wave on
seismic sections [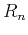 in equation (3)] is
described by the delta function, then, as follows from the known
properties of this function,
in equation (3)] is
described by the delta function, then, as follows from the known
properties of this function,
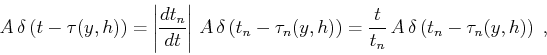 |
(56) |
which leads to the equality
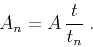 |
(57) |
Combining equation (57) with equations (54)
and (53) allows us to evaluate the amplitude after
continuation from some initial offset 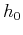 to another offset
to another offset 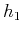 ,
as follows:
,
as follows:
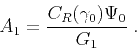 |
(58) |
According to equation (58), the OC process described by
equation (1) is amplitude-preserving in the sense
that corresponds to the definition of Born DMO
(Bleistein, 1990; Liner, 1991). This means that the geometric spreading
factor from the initial amplitudes is transformed to the true
geometric spreading on the continued section, while the reflection
coefficient stays the same. This remarkable dynamic property allows
AVO (amplitude versus offset) analysis to be performed by a dynamic
comparison between true constant-offset sections and the sections
transformed by OC from different offsets. With a simple trick, the
offset coordinate is transferred to the reflection angles for the AVO
analysis. As follows from (47) and (9),
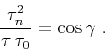 |
(59) |
If we include the
 factor in the DMO operator
(continuation to zero offset) and divide the result by the DMO section
obtained without this factor, the resultant amplitude of the reflected
events will be directly proportional to
factor in the DMO operator
(continuation to zero offset) and divide the result by the DMO section
obtained without this factor, the resultant amplitude of the reflected
events will be directly proportional to 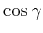 , where the
reflection angle
, where the
reflection angle 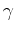 corresponds to the initial offset. Of
course, this conclusion is rigorously valid for constant-velocity
2.5-D media only.
corresponds to the initial offset. Of
course, this conclusion is rigorously valid for constant-velocity
2.5-D media only.
Black et al. (1993) suggest a definition of true-amplitude DMO different
from that of Born DMO. The difference consists of two important
components:
- True-amplitude DMO addresses preserving the peak amplitude
of the image wavelet instead of preserving its spectral density.
In the terms of this paper, the peak amplitude corresponds to the
pre-NMO amplitude
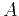 from formula (54) instead of
corresponding to the spectral density amplitude
from formula (54) instead of
corresponding to the spectral density amplitude 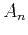 . A simple
correction factor
. A simple
correction factor 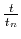 would help us take the difference
between the two amplitudes into account. Multiplication by
would help us take the difference
between the two amplitudes into account. Multiplication by 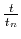 can be easily done at the NMO stage.
can be easily done at the NMO stage.
- Seismic sections are multiplied by time to correct for the
geometric spreading factor prior to DMO (or, in our case, offset
continuation) processing.
As follows
from (55), multiplication by 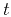 is a valid geometric
spreading correction for plane reflectors only. It is the
amplitude-preserving offset continuation based on the OC
equation (1) that is able to correct for the
curvature-dependent factor in the amplitude. To take into account the
second aspect of Black's definition, we can consider the modified
field
is a valid geometric
spreading correction for plane reflectors only. It is the
amplitude-preserving offset continuation based on the OC
equation (1) that is able to correct for the
curvature-dependent factor in the amplitude. To take into account the
second aspect of Black's definition, we can consider the modified
field 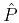 such that
such that
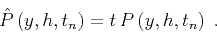 |
(60) |
Substituting (60) into the OC equation (1) transforms the
latter to the form
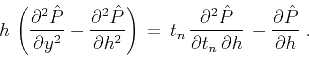 |
(61) |
Equations (61) and (1) differ
only with respect to the first-order damping term
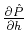 . This term affects the amplitude behavior but not
the traveltimes, since the eikonal-type equation (4)
depends on the second-order terms only. Offset continuation operators
based on (61) conform to Black's definition of
true-amplitude processing.
. This term affects the amplitude behavior but not
the traveltimes, since the eikonal-type equation (4)
depends on the second-order terms only. Offset continuation operators
based on (61) conform to Black's definition of
true-amplitude processing.
Fomel and Bleistein (2001) describe an alternative approach to
confirming the kinematic and amplitude validity of the offset
continuation equation. Applying equation (1)
directly on the Kirchhoff model of prestack seismic data shows that
the equation is satisfied to the same asymptotic order of accuracy
as the Kirchhoff modeling approximation (Bleistein, 1984; Haddon and Buchen, 1981).
 |
 |
 |
 | Theory of differential offset continuation |  |
![[pdf]](icons/pdf.png) |
Next: Integral offset continuation operator
Up: Introducing the offset continuation
Previous: Example 3: elliptic reflector
2014-03-26
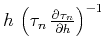 in equation (42) coincides
exactly with the time ray invariant
in equation (42) coincides
exactly with the time ray invariant ![\begin{eqnarray*}
\int_{t_o}^{t_n}\left[
h\,\left({\partial^2 \tau_n \over \par...
...artial \tau_n \over \partial h} \right)^{-1}\right]\,
d\tau_n =
\end{eqnarray*}](img136.png)