|
|
|
|
Theory of differential offset continuation |
In order to prove the validity of equation (4), it is
convenient to transform it to the coordinates of the initial shot
gathers: ![]() ,
, ![]() , and
, and
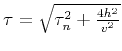 . The transformed equation takes the form
. The transformed equation takes the form
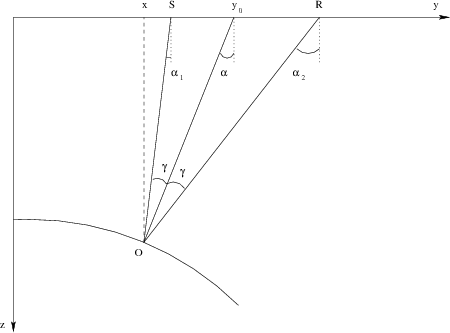
Let ![]() and
and ![]() be the source and the receiver locations, and
be the source and the receiver locations, and ![]() be a
reflection point for that pair. Note that the incident ray
be a
reflection point for that pair. Note that the incident ray ![]() and
the reflected ray
and
the reflected ray ![]() form a triangle with the basis on the offset
form a triangle with the basis on the offset
![]() (
(![]() ). Let
). Let ![]() be the angle of
be the angle of ![]() from the
vertical axis, and
from the
vertical axis, and ![]() be the analogous angle of
be the analogous angle of ![]() (Figure
1). The law of sines gives us the following explicit
relationships between the sides and the angles of the triangle
(Figure
1). The law of sines gives us the following explicit
relationships between the sides and the angles of the triangle ![]() :
:
|
ocoray
Figure 1. Reflection rays in a constant velocity medium (a scheme). |
|
|---|---|
|
|
Thus we have proved that equation (6), equivalent to (4), is valid in constant velocity media independently of the reflector geometry and the offset. This means that high-frequency asymptotic components of the waves, described by the OC equation, are located on the true reflection traveltime curves.
The theory of characteristics can provide other ways to prove the kinematic validity of equation (4), as described by Fomel (1994) and Goldin (1994).
|
|
|
|
Theory of differential offset continuation |