 |
 |
 |
 | Nonhyperbolic reflection moveout of 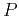 -waves:
An overview and comparison of reasons -waves:
An overview and comparison of reasons |  |
![[pdf]](icons/pdf.png) |
Next: Conclusions
Up: Fomel & Grechka: Nonhyperbolic
Previous: Curved reflector beneath homogeneous
The nonhyperbolic moveout in homogeneous VTI media with one horizontal reflector
is similar to that caused by lateral heterogeneity in isotropic models.
In this section, we discuss this similarity following the results of
Grechka (1998).
The angle dependence of the group velocity in equations (1)
and (5) is characterized by small anisotropic
coefficients. Therefore, we can assume that an analogous influence of
lateral heterogeneity might be caused by small
anisotropic
coefficients. Therefore, we can assume that an analogous influence of
lateral heterogeneity might be caused by small velocity
perturbations. (Large lateral velocity changes can cause behavior too
complicated for analytic description.) An appropriate model is a plane
laterally heterogeneous layer with the velocity
velocity
perturbations. (Large lateral velocity changes can cause behavior too
complicated for analytic description.) An appropriate model is a plane
laterally heterogeneous layer with the velocity
![\begin{displaymath}
V(y) = V_0 \left[ 1 + c(y) \right]\;,
\end{displaymath}](img178.png) |
(78) |
where 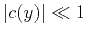 is a dimensionless function. The velocity
is a dimensionless function. The velocity 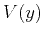 given by equation (78) has the generic perturbation
form that allows us to use the tomographic linearization assumption.
That is, we neglect the ray bending caused by the small velocity
perturbation
given by equation (78) has the generic perturbation
form that allows us to use the tomographic linearization assumption.
That is, we neglect the ray bending caused by the small velocity
perturbation 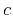 and compute the perturbation of traveltimes along
straight rays in the constant-velocity background. Thus, we can rewrite
equation (9) as
and compute the perturbation of traveltimes along
straight rays in the constant-velocity background. Thus, we can rewrite
equation (9) as
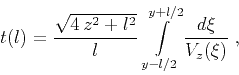 |
(79) |
where 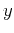 is the midpoint location and the integration limits correspond
to the source and receiver locations. For simplicity and without loss
of generality, we can set
is the midpoint location and the integration limits correspond
to the source and receiver locations. For simplicity and without loss
of generality, we can set 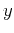 to zero. Linearizing equation (79)
with respect to the small perturbation
to zero. Linearizing equation (79)
with respect to the small perturbation 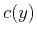 , we get
, we get
![\begin{displaymath}
t(l) = { \sqrt{4 z^2 + l^2} \over V_0 } \left[ 1 - {1 \over {l}}
\int\limits_{-l/2}^{l/2} c(\xi) d\xi \right]\;.
\end{displaymath}](img184.png) |
(80) |
It is clear from equation (80) that lateral
heterogeneity can cause many different types of the nonhyperbolic moveout.
In particular, comparing equations (80) and
(11), we conclude that a pseudo-anisotropic behavior of
traveltimes is produced by lateral heterogeneity in the form
![\begin{displaymath}
c(l) = { d \over {d l}}
\left[{ {l^3 (l^2 \epsilon + 4 z^2 \delta )} \over
{(l^2 + 4 z^2)^2} } \right]
\end{displaymath}](img185.png) |
(81) |
or, in the linear approximation,
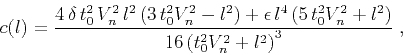 |
(82) |
where 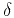 and
and 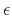 should be considered now as
parameters, describing the isotropic
should be considered now as
parameters, describing the isotropic laterally heterogeneous velocity
field. Equation (82) indicates that the velocity heterogeneity
laterally heterogeneous velocity
field. Equation (82) indicates that the velocity heterogeneity
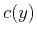 that reproduces moveout (12) in a homogeneous VTI medium,
is a symmetric function of the offset
that reproduces moveout (12) in a homogeneous VTI medium,
is a symmetric function of the offset 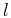 . This is not surprising
because the velocity function (1), corresponding to vertical
transverse isotropy, is symmetric as well.
. This is not surprising
because the velocity function (1), corresponding to vertical
transverse isotropy, is symmetric as well.
 |
 |
 |
 | Nonhyperbolic reflection moveout of  -waves:
An overview and comparison of reasons -waves:
An overview and comparison of reasons |  |
![[pdf]](icons/pdf.png) |
Next: Conclusions
Up: Fomel & Grechka: Nonhyperbolic
Previous: Curved reflector beneath homogeneous
2013-03-03
![]() anisotropic
coefficients. Therefore, we can assume that an analogous influence of
lateral heterogeneity might be caused by small
anisotropic
coefficients. Therefore, we can assume that an analogous influence of
lateral heterogeneity might be caused by small![]() velocity
perturbations. (Large lateral velocity changes can cause behavior too
complicated for analytic description.) An appropriate model is a plane
laterally heterogeneous layer with the velocity
velocity
perturbations. (Large lateral velocity changes can cause behavior too
complicated for analytic description.) An appropriate model is a plane
laterally heterogeneous layer with the velocity