 |
 |
 |
 | Nonhyperbolic reflection moveout of 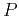 -waves:
An overview and comparison of reasons -waves:
An overview and comparison of reasons |  |
![[pdf]](icons/pdf.png) |
Next: HORIZONTAL REFLECTOR BENEATH A
Up: Fomel & Grechka: Nonhyperbolic
Previous: Introduction
In transversely isotropic media, velocities of seismic waves depend
on the direction of propagation measured from the symmetry
axis. Thomsen (1986) introduced a notation for VTI
media by replacing the elastic stiffness coefficients
with the 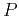 - and
- and 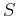 -wave velocities along the symmetry
axis and three dimensionless anisotropic parameters. As shown by Tsvankin
(Tsvankin, 1996), the
-wave velocities along the symmetry
axis and three dimensionless anisotropic parameters. As shown by Tsvankin
(Tsvankin, 1996), the 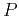 -wave seismic signatures in
VTI media can be conveniently expressed in terms of
Thomsen's parameters
-wave seismic signatures in
VTI media can be conveniently expressed in terms of
Thomsen's parameters 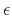 and
and 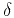 .
Deviations of these parameters from zero characterize the relative
strength of anisotropy. For small values of these parameters,the
weak-anisotropy approximation (Thomsen, 1986; Tsvankin and Thomsen, 1994)
reduces to simple linearization.
.
Deviations of these parameters from zero characterize the relative
strength of anisotropy. For small values of these parameters,the
weak-anisotropy approximation (Thomsen, 1986; Tsvankin and Thomsen, 1994)
reduces to simple linearization.
The squared group velocity
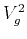 of
of 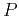 -waves in weakly anisotropic VTI media can be expressed
as a function of the group angle
-waves in weakly anisotropic VTI media can be expressed
as a function of the group angle 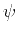 measured from the vertical
symmetry axis as follows:
measured from the vertical
symmetry axis as follows:
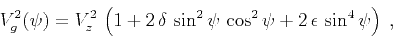 |
(1) |
where 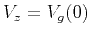 is the
is the  -wave vertical velocity, and
-wave vertical velocity, and 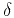 and
and
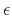 are Thomsen's dimensionless anisotropic parameters, which
are assumed to be small quantities:
are Thomsen's dimensionless anisotropic parameters, which
are assumed to be small quantities:
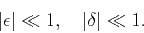 |
(2) |
Both parameters are equal to zero in isotropic media.
Equation (1) is accurate up to the second-order terms in
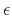 and
and 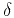 . We retain this level of accuracy throughout
the paper. As follows from equation
(1), the velocity
. We retain this level of accuracy throughout
the paper. As follows from equation
(1), the velocity 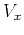 corresponding to ray
propagation in the horizontal direction is
corresponding to ray
propagation in the horizontal direction is
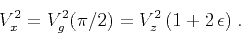 |
(3) |
Equation (3) is actually exact, valid
for any strength of anisotropy. Another important quantity is the
normal-moveout (NMO) velocity, 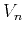 , that determines the small-offset
, that determines the small-offset
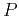 -wave reflection moveout in homogeneous VTI media above a
horizontal reflector. Its exact expression is (Thomsen, 1986)
-wave reflection moveout in homogeneous VTI media above a
horizontal reflector. Its exact expression is (Thomsen, 1986)
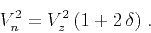 |
(4) |
If 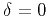 as, for example, in the ANNIE model proposed by
Schoenberg et al. (1996), the normal-moveout velocity
is equal to the vertical velocity.
as, for example, in the ANNIE model proposed by
Schoenberg et al. (1996), the normal-moveout velocity
is equal to the vertical velocity.
It is convenient to rewrite equation (1) in the form
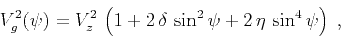 |
(5) |
where
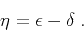 |
(6) |
Equation (6) is the weak-anisotropy approximation for the
anellipticity coefficient
coefficient 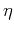 introduced by
Alkhalifah and Tsvankin (1995). For the elliptic anisotropy,
introduced by
Alkhalifah and Tsvankin (1995). For the elliptic anisotropy,
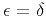 and
and
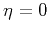 . To see why the group-velocity function becomes elliptic in
this case, note that for small
. To see why the group-velocity function becomes elliptic in
this case, note that for small 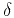
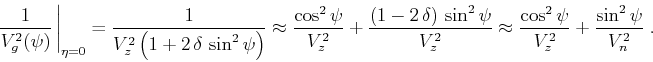 |
(7) |
Seismic data often indicate that
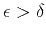 , so the anellipticity
coefficient
, so the anellipticity
coefficient 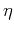 is usually positive.
is usually positive.
An equivalent form of equation (1) can be obtained in terms of
the three characteristic velocities 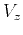 ,
, 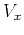 , and
, and 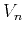 :
:
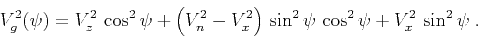 |
(8) |
From equation (8), in the linear
approximation the anelliptic behavior of velocity is controlled by
the difference between the normal moveout and horizontal velocities
or, equivalently, by the difference between anisotropic
coefficients 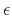 and
and 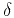 .
.
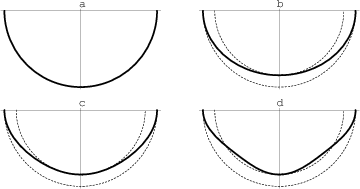
We illustrate different types of the group velocities (wavefronts)
in Figure 1.
The wavefront, circular in the isotropic case (Figure
1a), becomes elliptical when
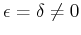 (Figure 1b). In the ANNIE model, the vertical and NMO
velocities are equal (Figure 1c). If
(Figure 1b). In the ANNIE model, the vertical and NMO
velocities are equal (Figure 1c). If 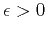 and
and
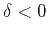 , the three characteristic velocities satisfy the
inequality
, the three characteristic velocities satisfy the
inequality
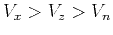 (Figure 1d).
(Figure 1d).
|
|---|
nmofro
Figure 1. Wavefronts in
isotropic medium,
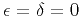 (a),
elliptically anisotropic medium, (a),
elliptically anisotropic medium,
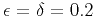 (b),
ANNIE model, (b),
ANNIE model, 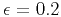 , , 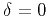 (c), and
anisotropic medium with (c), and
anisotropic medium with 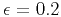 , , 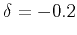 (d).
Solid curves represent the wavefronts.
Dashed lines correspond to isotropic wavefronts for the vertical and
horizontal velocities. (d).
Solid curves represent the wavefronts.
Dashed lines correspond to isotropic wavefronts for the vertical and
horizontal velocities.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[mathematica]](icons/mathematica.png)
|
|---|
 |
 |
 |
 | Nonhyperbolic reflection moveout of 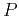 -waves:
An overview and comparison of reasons -waves:
An overview and comparison of reasons |  |
![[pdf]](icons/pdf.png) |
Next: HORIZONTAL REFLECTOR BENEATH A
Up: Fomel & Grechka: Nonhyperbolic
Previous: Introduction
2013-03-03
![]() of
of ![]() -waves in weakly anisotropic VTI media can be expressed
as a function of the group angle
-waves in weakly anisotropic VTI media can be expressed
as a function of the group angle ![]() measured from the vertical
symmetry axis as follows:
measured from the vertical
symmetry axis as follows:
![]() and
and ![]() . We retain this level of accuracy throughout
the paper. As follows from equation
(1), the velocity
. We retain this level of accuracy throughout
the paper. As follows from equation
(1), the velocity ![]() corresponding to ray
propagation in the horizontal direction is
corresponding to ray
propagation in the horizontal direction is
![]() ,
, ![]() , and
, and ![]() :
:
![]() (Figure 1b). In the ANNIE model, the vertical and NMO
velocities are equal (Figure 1c). If
(Figure 1b). In the ANNIE model, the vertical and NMO
velocities are equal (Figure 1c). If ![]() and
and
![]() , the three characteristic velocities satisfy the
inequality
, the three characteristic velocities satisfy the
inequality
![]() (Figure 1d).
(Figure 1d).
