 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Low-frequency waves in 3D
Up: Browaeys & Fomel: Fractals
Previous: Seismic-scale heterogeneities
Different scattering regimes exist when waves propagate in heterogeneous media,
according to the ratio of the wavelength, 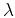 , to the size,
, to the size, 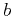 , of heterogeneities.
The formalism including the different scattering regimes,
when heterogeneities are modeled by spherical inclusions,
is the Mie scattering theory.
Recent experimental results
(Le Gonidec and Gibert, 2007)
on sonic-wave reflectivity in a granular medium,
made up of beads of size
, of heterogeneities.
The formalism including the different scattering regimes,
when heterogeneities are modeled by spherical inclusions,
is the Mie scattering theory.
Recent experimental results
(Le Gonidec and Gibert, 2007)
on sonic-wave reflectivity in a granular medium,
made up of beads of size 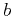 in a water tank, illustrate this classification :
in a water tank, illustrate this classification :
- for low frequencies, when
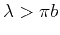 , backward scattering is dominant,
the Born approximation can be used, and the regime is Rayleigh scattering;
, backward scattering is dominant,
the Born approximation can be used, and the regime is Rayleigh scattering;
- for wavelengths similar in size to heterogeneity, when
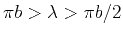 ,
lateral scattering is important, multiples should not be neglected,
and the regime is called resonant scattering; and
,
lateral scattering is important, multiples should not be neglected,
and the regime is called resonant scattering; and
- for high frequencies, when
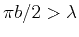 , waves are scattered mainly forward, and
localization theory and the Rytov formalism are appropriate.
, waves are scattered mainly forward, and
localization theory and the Rytov formalism are appropriate.
Experiments have demonstrated that wave reflectivity strongly decreases
when the wavelength of the incident wave is twice the diameter of the beads,
for which lateral scattering starts to be dominant.
Mean wavefield formalism is valid only for a low frequency,
when the wavelength is larger than the size of heterogeneities
because of the assumptions in the derivation (Karal and Keller, 1964).
The Born approximation can describe the Rayleigh regime and the approach of resonant phase scattering (Frankel and Clayton, 1986; Sato and Fehler, 1998).
For wavelengths shorter than the size of heterogeneities,
artificial decoherence by phase randomization occurs (Sato and Fehler, 1998; Wu, 1982).
We intend to describe the 3D attenuation in a stochastic fractal medium,
when 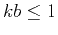 , which is relevant for seismic survey frequencies.
The limit of validity corresponds to wavelengths approaching the size of heterogeneities.
We assume heterogeneities to be isotropic.
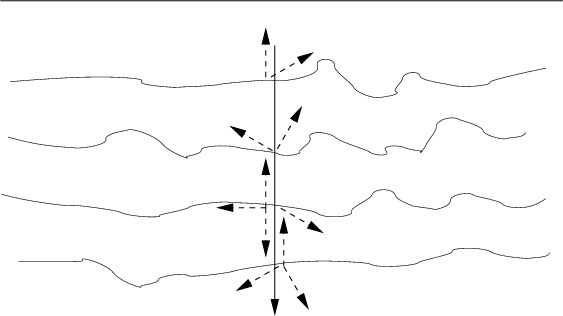
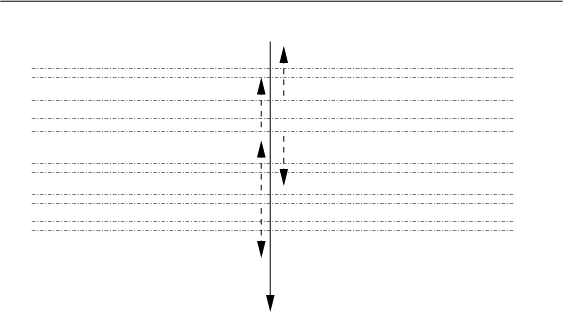
The schemes in Figure 5
compare a realistic geological structure
with two different end-member models.
Scattering calculations in 1D underestimate the scattering loss by small-scale heterogeneities.
, which is relevant for seismic survey frequencies.
The limit of validity corresponds to wavelengths approaching the size of heterogeneities.
We assume heterogeneities to be isotropic.
The schemes in Figure 5
compare a realistic geological structure
with two different end-member models.
Scattering calculations in 1D underestimate the scattering loss by small-scale heterogeneities.

|
|---|
schemescatter3dgg,schemescatterd,schemescatter3d
Figure 5. Schematic comparison of single scattering effects,
during a vertical wave propagation in sediments,
between a realistic geological structure (a) and two end-member models:
horizontal layers with propagation including 1D scattering (b)
and isotropic heterogeneities with 3D scattering (c).
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[xfig]](icons/xfig.png) ![[xfig]](icons/xfig.png) ![[xfig]](icons/xfig.png)
|
|---|
Subsections
 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Low-frequency waves in 3D
Up: Browaeys & Fomel: Fractals
Previous: Seismic-scale heterogeneities
2013-03-02
![]() , to the size,
, to the size, ![]() , of heterogeneities.
The formalism including the different scattering regimes,
when heterogeneities are modeled by spherical inclusions,
is the Mie scattering theory.
Recent experimental results
(Le Gonidec and Gibert, 2007)
on sonic-wave reflectivity in a granular medium,
made up of beads of size
, of heterogeneities.
The formalism including the different scattering regimes,
when heterogeneities are modeled by spherical inclusions,
is the Mie scattering theory.
Recent experimental results
(Le Gonidec and Gibert, 2007)
on sonic-wave reflectivity in a granular medium,
made up of beads of size ![]() in a water tank, illustrate this classification :
in a water tank, illustrate this classification :


