 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Attenuation in 3D fractal
Up: Scattering attenuation in 3D
Previous: Scattering attenuation in 3D
A scalar wave
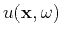 in a weakly inhomogeneous medium
(Karal and Keller, 1964; Chernov, 1960; Tatarski, 1961)
satisfies the Helmholtz wave equation
in a weakly inhomogeneous medium
(Karal and Keller, 1964; Chernov, 1960; Tatarski, 1961)
satisfies the Helmholtz wave equation
where 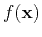 is a small perturbation of the medium from homogeneity, and
is a small perturbation of the medium from homogeneity, and
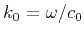 .
Phase velocity
.
Phase velocity 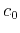 is the background velocity.
Assuming a second-order stationary statistical distribution
for fluctuations
is the background velocity.
Assuming a second-order stationary statistical distribution
for fluctuations 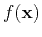 and a zero expectation value
and a zero expectation value
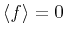 , spatial covariance of the velocity variations is
defined by relation 1.
Expectation
, spatial covariance of the velocity variations is
defined by relation 1.
Expectation
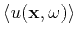 of random plane-wave realizations
is calculated (Karal and Keller, 1964)
using a perturbation theory to the second order in
of random plane-wave realizations
is calculated (Karal and Keller, 1964)
using a perturbation theory to the second order in 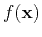 by
by
![$\displaystyle \left[\Delta+k_0^2(1+\sigma^2)\right]\langle u(\mathbf{x},\omega)...
...mega)
\,\langle u(\mathbf{x}^{\prime},\omega)\rangle~d\mathbf{x}^{\prime}= 0\,,$](img152.png) |
|
|
(17) |
where
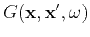 is Green's function of the operator
is Green's function of the operator
![$\left[\Delta+k_0^2\right]$](img154.png) ,
and integration is performed over the 3D space.
The dispersion relation for a plane wave propagating in the heterogeneous medium follows as
,
and integration is performed over the 3D space.
The dispersion relation for a plane wave propagating in the heterogeneous medium follows as
where
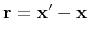 is the relative position, with an absolute value
is the relative position, with an absolute value
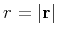 ,
and
,
and
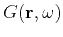 is the 3D isotropic free-space Green's function with the outward radiation condition
(Bleistein et al., 2001).
The path of waves should be sufficiently long to significantly sample medium heterogeneities statistically (Gist, 1994).
The Born approximation is present because of Green's function.
Heterogeneities with the isotropic correlation function
is the 3D isotropic free-space Green's function with the outward radiation condition
(Bleistein et al., 2001).
The path of waves should be sufficiently long to significantly sample medium heterogeneities statistically (Gist, 1994).
The Born approximation is present because of Green's function.
Heterogeneities with the isotropic correlation function 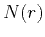 produce an isotropic wave vector
produce an isotropic wave vector 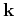 .
Combining Green's function in equation 19 with the isotropic integral in equation 5 reduces
the squared dispersion relation of equation 18 to
.
Combining Green's function in equation 19 with the isotropic integral in equation 5 reduces
the squared dispersion relation of equation 18 to
Second-order expansion
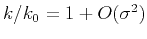 in the solution constrains validity to the domain
in the solution constrains validity to the domain
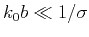 , where
, where 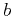 is the characteristic length scale of the heterogeneities.
The second-order approximation for the 3D dispersion relation is finally
is the characteristic length scale of the heterogeneities.
The second-order approximation for the 3D dispersion relation is finally
Quantity 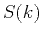 , introduced above, is related to the real and even function
, introduced above, is related to the real and even function 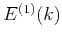 , defined by the isotropic integral of equation 4:
, defined by the isotropic integral of equation 4:
Connection to the O'Doherty-Anstey formula is detailed in Appendix A.
 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Attenuation in 3D fractal
Up: Scattering attenuation in 3D
Previous: Scattering attenuation in 3D
2013-03-02
![]() in a weakly inhomogeneous medium
(Karal and Keller, 1964; Chernov, 1960; Tatarski, 1961)
satisfies the Helmholtz wave equation
in a weakly inhomogeneous medium
(Karal and Keller, 1964; Chernov, 1960; Tatarski, 1961)
satisfies the Helmholtz wave equation
![$\displaystyle \left[\Delta+k_0^2(1+\sigma^2)\right]\langle u(\mathbf{x},\omega)...
...mega)
\,\langle u(\mathbf{x}^{\prime},\omega)\rangle~d\mathbf{x}^{\prime}= 0\,,$](img152.png)
![$\displaystyle 1 + \sigma^2\left[1 - \frac{4\,k_0^2}{k}\int_{0}^{\infty}\hspace{-2mm} N(r)\,e^{ik_0r}\sin(kr)\,dr\right].$](img162.png)