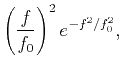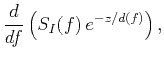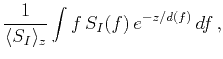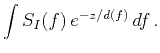|
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Discussion
Up: Attenuation in 3D fractal
Previous: Penetration depth
If seismic pulse is defined as a Ricker wavelet, a relation can be derived for
modification of the frequency content of P and S acoustic waves by scattering attenuation.
Dominant frequency  with depth
with depth 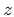 and initial spectrum
and initial spectrum 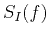 of the source are defined by
of the source are defined by
with initial condition
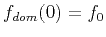 , and where
, and where 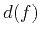 is the penetration depth
defined in equation 34.
Dispersion involves different traveltimes
at different frequencies but does not modify the frequency content or amplitude.
For convenience, we estimate dominant frequency as frequency expectation:
is the penetration depth
defined in equation 34.
Dispersion involves different traveltimes
at different frequencies but does not modify the frequency content or amplitude.
For convenience, we estimate dominant frequency as frequency expectation:
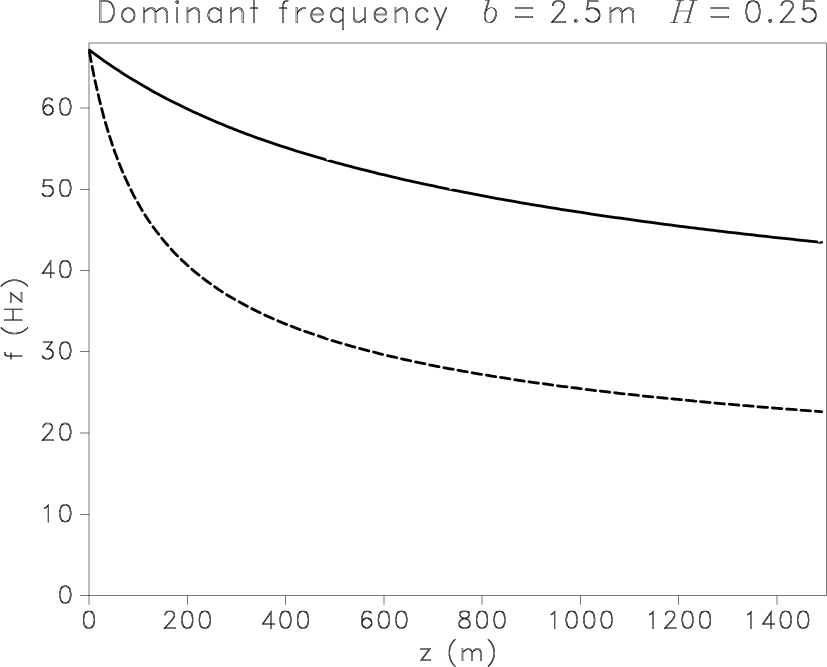
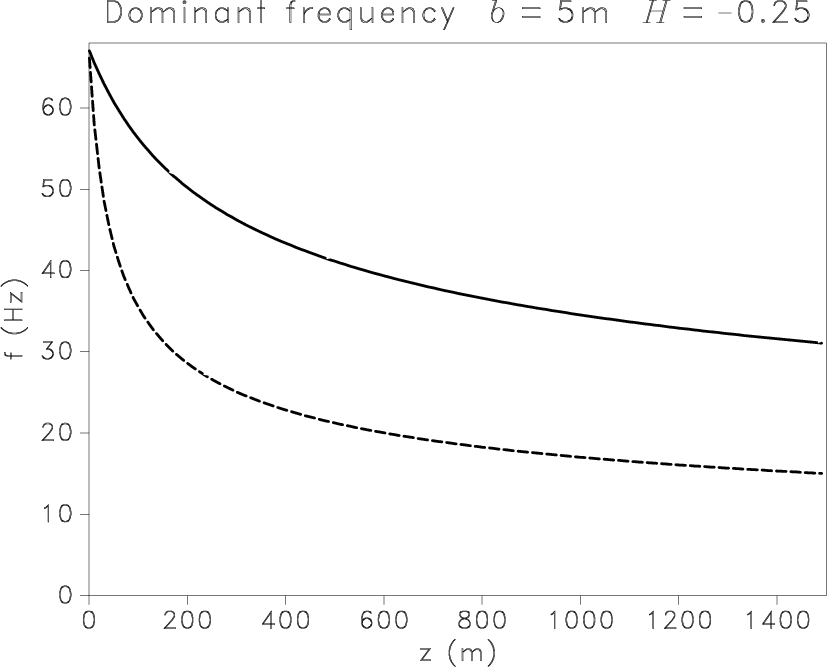
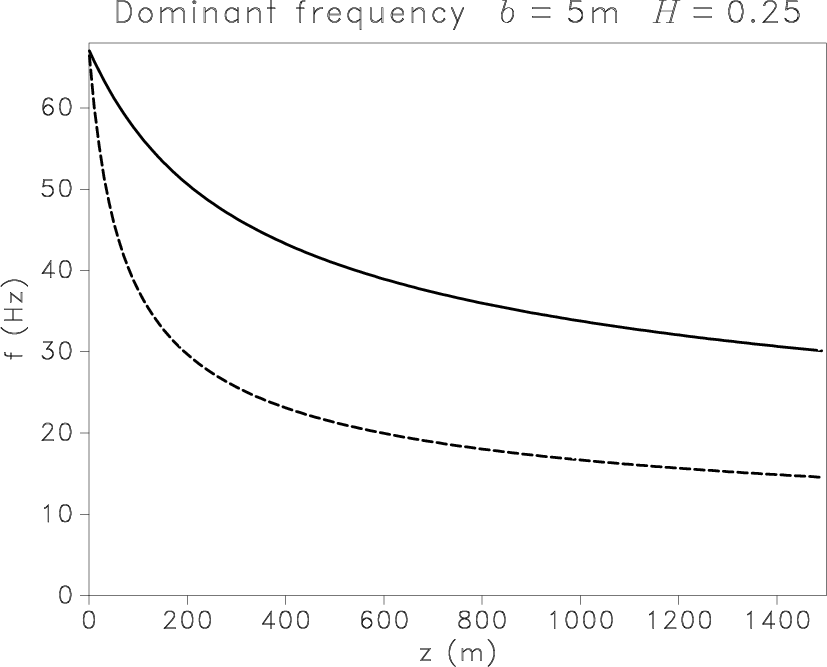
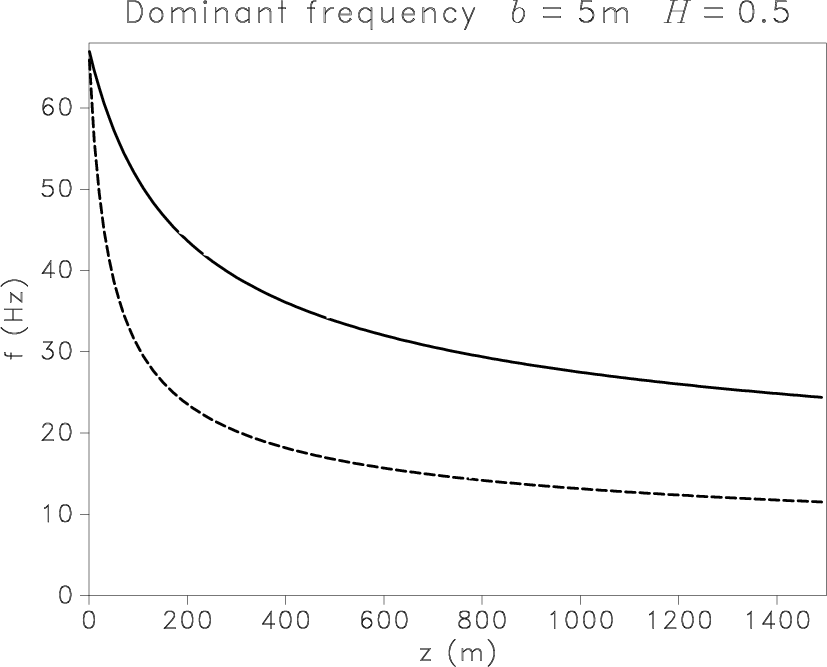
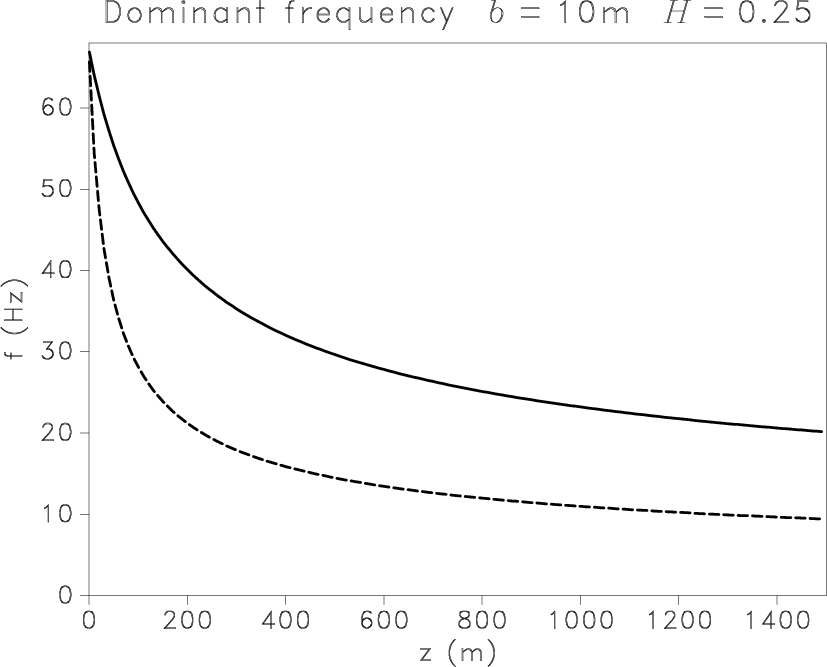
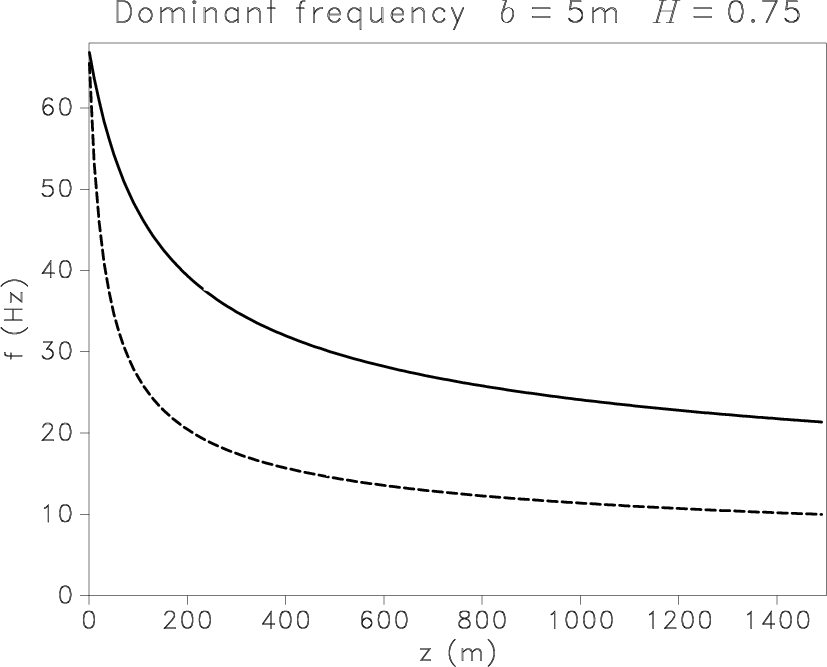
Figure 8
shows the evolution of the dominant frequency with depth
in fractal media, with 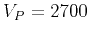 m/s,
m/s, 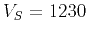 m/s, and standard deviation
m/s, and standard deviation 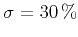 .
The value of correlation length
.
The value of correlation length 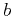 again has a very high impact,
whereas the fractal exponent moderately influences results.
For a multicomponent seismic survey in a clastic reservoir,
evolution of the peak frequency should show a more
important decrease with depth for PS data than for PP data.
again has a very high impact,
whereas the fractal exponent moderately influences results.
For a multicomponent seismic survey in a clastic reservoir,
evolution of the peak frequency should show a more
important decrease with depth for PS data than for PP data.
|
|---|
fdomfb25025,fdomfb05M025,fdomfb05025,fdomfb0505,fdomfb10025,fdomfb05075
Figure 8. Evolution of the dominant frequency with depth for P (solid line) and S (dashed line) scalar waves modeled by a Ricker wavelet (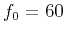 Hz)
in heterogeneous media with Hz)
in heterogeneous media with 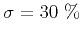 . For a constant exponent . For a constant exponent 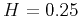 ,
the dominant frequency shifts to lower frequencies faster for larger values of ,
the dominant frequency shifts to lower frequencies faster for larger values of 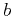 (a,c,e).
The exponent (a,c,e).
The exponent 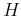 weakly influences the evolution of the dominant frequency (b,d,f). weakly influences the evolution of the dominant frequency (b,d,f).
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Discussion
Up: Attenuation in 3D fractal
Previous: Penetration depth
2013-03-02
![]() with depth
with depth ![]() and initial spectrum
and initial spectrum ![]() of the source are defined by
of the source are defined by