|
|
|
|
Fractal heterogeneities in sonic logs and low-frequency scattering attenuation |
The attenuation caused by anticorrelated 3D small-scale heterogeneities can be explained by a low-frequency scattering theory. The length scales that we estimated from sonic logs justify this approach for conventional seismic frequencies. The intensity of scattering attenuation and the value of frequency cutoff strongly depend on the size of the heterogeneities, and S-waves are more attenuated than P-waves at the same frequency. Using low-frequency P-waves provides a better depth of penetration. More reflectors can be detected and imaged, but, of course, with less resolution. This phenomenon was observed in sub-basalt imaging (Ziolkowski et al., 2003). Our analysis of sonic logs confirms the relevance of a fractal description for the high-frequency content of quasi-periodic geological layers. Because sediments are highly stratified, their layered structure has previously motivated use of 1D models for seismic scattering attenuation, but a realistic estimate needs to be conducted in 3D. More generally, description of geological heterogeneities and use of scattering theories should be as depicted in Figure 7.
Several limitations should be pointed out in our study.
Well logs constitute 1D samples of the geological medium in the near vertical direction.
Use of 3D isotropy is the simplest assumption
consistent with our limited knowledge.
We consequently ignore the anisotropic effect of layering, which undoubtly affects lateral scattering when ![]() .
Also note that the relation between fractal exponent
.
Also note that the relation between fractal exponent ![]() and parameter
and parameter ![]() depends on spatial dimension
depends on spatial dimension ![]() .
We have therefore proposed different values of parameter
.
We have therefore proposed different values of parameter ![]() for depth of penetration and evolution of dominant frequency
in Figures 6
and 8
and have attempted to extract some general trends.
for depth of penetration and evolution of dominant frequency
in Figures 6
and 8
and have attempted to extract some general trends.
Our analysis is limited by the fact that we used variations of the
seismic velocity, but not of density, in order to be consistent with
the mean field theory. This theory retrieves the Backus limit and the
Rayleigh diffusion regime. Fortunately, densities commonly exhibit
fewer variations. Meanwhile, analysis of the logarithm of impedance
![]() relates directly to the reflection coefficients
(Shtatland, 1991). Backscattering is known to be related to
impedance fluctuations (Wu, 1988; Banik et al., 1985). Modification of the
Helmholtz equation (16) in 1D to incorporate
relates directly to the reflection coefficients
(Shtatland, 1991). Backscattering is known to be related to
impedance fluctuations (Wu, 1988; Banik et al., 1985). Modification of the
Helmholtz equation (16) in 1D to incorporate ![]() was
succesfully achieved by Banik et al. (1985), and they provided a proof
of O'Doherty-Anstey formula. Impedance
was
succesfully achieved by Banik et al. (1985), and they provided a proof
of O'Doherty-Anstey formula. Impedance ![]() , depending on depth
, depending on depth
![]() , and reflection coefficient series
, and reflection coefficient series ![]() are connected by
are connected by
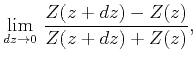 |
(39) | ||
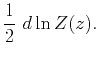 |
(40) |
|
|
|
|
Fractal heterogeneities in sonic logs and low-frequency scattering attenuation |