 |
 |
 |
 | Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |  |
![[pdf]](icons/pdf.png) |
Next: Pseudo-pure-mode qP-wave equation in
Up: PSEUDO-PURE-MODE COUPLED SYSTEM FOR
Previous: Plane-wave analysis of the
To describe propagation of separated qP-waves in anisotropic media, we first revisit the classical wave mode
separation theory. In isotropic media, scalar P-wave can be separated from the extrapolated
vector wavefield
 by applying a divergence operation:
by applying a divergence operation:
 .
In the wavenumber domain,
this can be equivalently expressed as a dot product that essentially projects the wavefield
.
In the wavenumber domain,
this can be equivalently expressed as a dot product that essentially projects the wavefield
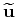 onto the wave vector
onto the wave vector
 , i.e.,
, i.e.,
 |
(8) |
Similarly, for an anisotropic medium, scalar qP-waves can be separated
by projecting the vector wavefields onto the true polarization
directions of qP-waves by
(Dellinger and Etgen, 1990),
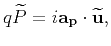 |
(9) |
where
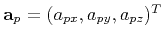 represents the polarization vector for qP-waves.
For heterogeneous models, this scalar projection can be performed using
nonstationary spatial filtering depending on local material parameters (Yan and Sava, 2009).
represents the polarization vector for qP-waves.
For heterogeneous models, this scalar projection can be performed using
nonstationary spatial filtering depending on local material parameters (Yan and Sava, 2009).
To provide more flexibility for characterizing wave propagation in anisotropic media, we suggest to split
the one-step projection into two steps, of which the first step
implicitly implements partail wave mode separation (like in equation 8) during wavefield
extrapolation with a transformed wave equation, while the second step is designed to correct the
projection deviation implied by equations 8 and 9.
We achieve this on the base of the following observations:
the difference of the polarization between an ordinary anisotropic medium and its isotropic reference
at a given wave vector direction is usually
small, though exceptions are possible (Tsvankin and Chesnokov, 1990; Thomsen, 1986); The wave vector can be
taken as the isotropic reference of the polarization vector for qP-waves; It is a material-independent
operation to project the elastic wavefield onto the wave vector.
Therefore, we introduce a similarity transformation to the Christoffel matrix, i.e.,
 |
(10) |
with a invertible 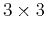 matrix
matrix
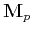 related to the wave vector:
related to the wave vector:
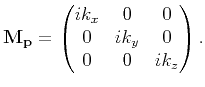 |
(11) |
Accordingly, we derive an equivalent Christoffel equation,
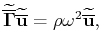 |
(12) |
for a transformed wavefield:
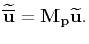 |
(13) |
The above similarity transformation does not change the eigeinvalues of the Christoffel matrix and thus
introduces no kinematic errors for the wavefields. By the way, we can obtain
the same transformed Christoffel equation if matrix
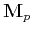 is constructed using the normalized wavenumbers
to ensure all spatial frequencies are uniformly scaled.
For a locally smooth medium, applying an inverse Fourier transform to
equation 12, we obtain a coupled
linear second-order system kinematically equivalent to the original elastic wave equation:
is constructed using the normalized wavenumbers
to ensure all spatial frequencies are uniformly scaled.
For a locally smooth medium, applying an inverse Fourier transform to
equation 12, we obtain a coupled
linear second-order system kinematically equivalent to the original elastic wave equation:
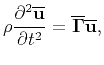 |
(14) |
where
 represents the time-space domain wavefields, and
represents the time-space domain wavefields, and
 represents the Christoffel differential-operator matrix after the similarity transformation.
represents the Christoffel differential-operator matrix after the similarity transformation.
For the transformed elastic wavefield in the wavenumber-domain, we have
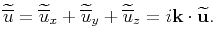 |
(15) |
And in space-domain, we also have
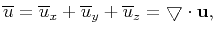 |
(16) |
with
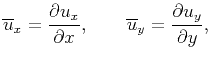 and and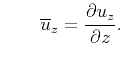 |
(17) |
These imply that the new wavefield components essentially represent the spatial derivatives of the original
components of the displacement wavefield, and the transformation (equation 13)
plus the summation of the transformed wavefield components (like in equation 15 or 16)
essentially finishes a scalar projection of the displacement wavefield onto the wave vector.
For isotropic media, such a projection directly produces scalar P-wave data. In an anisotropic medium,
however, only a partial wave-mode separation is achieved becuase there is usually a direction deviation
between the wave vector and the polarization vector of qP-wave.
Generally, this deviation turns out to be small and
its maximum value rarely exceeds 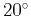 for typical anisotropic earth media(Psencik and Gajewski, 1998).
Because of the orthognality of qP- and qS-wave polarizations, the projection deviations of qP-waves are generally
far less than those of the qSV-waves when the elastic wavefields are projected onto the isotropic references
of the qP-wave's polarization vectors.
As demonstrated in the synthetic examples of various symmetry and strength of anisotropy,
the scalar wavefield
for typical anisotropic earth media(Psencik and Gajewski, 1998).
Because of the orthognality of qP- and qS-wave polarizations, the projection deviations of qP-waves are generally
far less than those of the qSV-waves when the elastic wavefields are projected onto the isotropic references
of the qP-wave's polarization vectors.
As demonstrated in the synthetic examples of various symmetry and strength of anisotropy,
the scalar wavefield
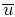 represents dominantly
the energy of qP-waves but contains some weak residual qS-waves.
This is why we call the coupled system (equation 14) a pseudo-pure-mode wave equation
for qP-wave in anisotropic media.
represents dominantly
the energy of qP-waves but contains some weak residual qS-waves.
This is why we call the coupled system (equation 14) a pseudo-pure-mode wave equation
for qP-wave in anisotropic media.
Substituting the corresponding stiffness matrix into the above derivations, we get the extended expression of
pseudo-pure-mode qP-wave equation for any anisotropic media.
As demonstrated in Appendix A, pseudo-pure-mode qP-wave equation in vertical TI and orthorhombic media can be expressed as
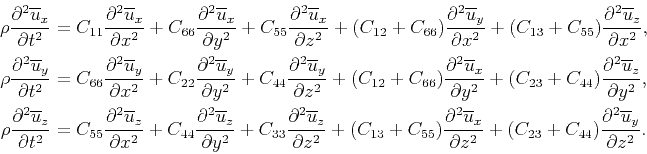 |
(18) |
Note that, unlike the original elastic wave equation, pseudo-pure-mode wave equation dose not contain mixed partial
derivatives.
This is a good news because it takes more computational cost to compute the mixed partial derivatives
using a finite-difference algorithm with required accuracy.
In the forthcoming text, we focus on demonstration of pseudo-pure-mode qP-wave equations for TI media while
briefly supplement similar derivation for orthorhombic media in Appendix B.
Subsections
 |
 |
 |
 | Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |  |
![[pdf]](icons/pdf.png) |
Next: Pseudo-pure-mode qP-wave equation in
Up: PSEUDO-PURE-MODE COUPLED SYSTEM FOR
Previous: Plane-wave analysis of the
2014-06-24