|
|
|
|
Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |
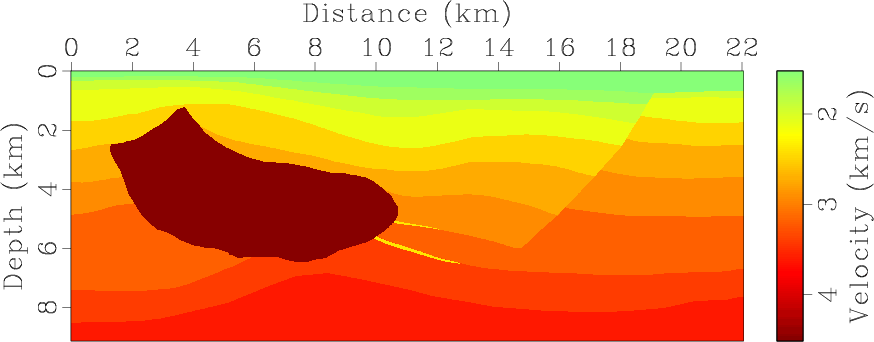
Then we demonstrate the approach in the 2D Hess VTI model (Figure 7).
Vertical S-wave velocity is set to equal half the vertical P-wave velocity everywhere. A point-source is placed
at location of (13.264, 4.023) km.
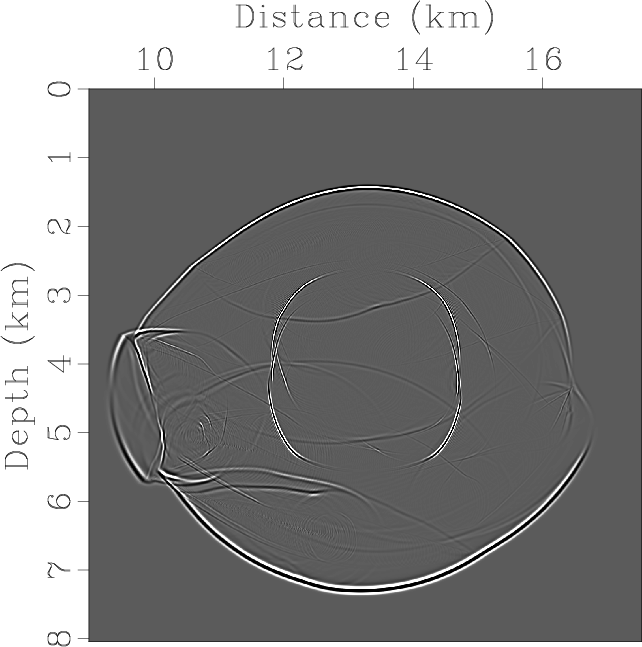
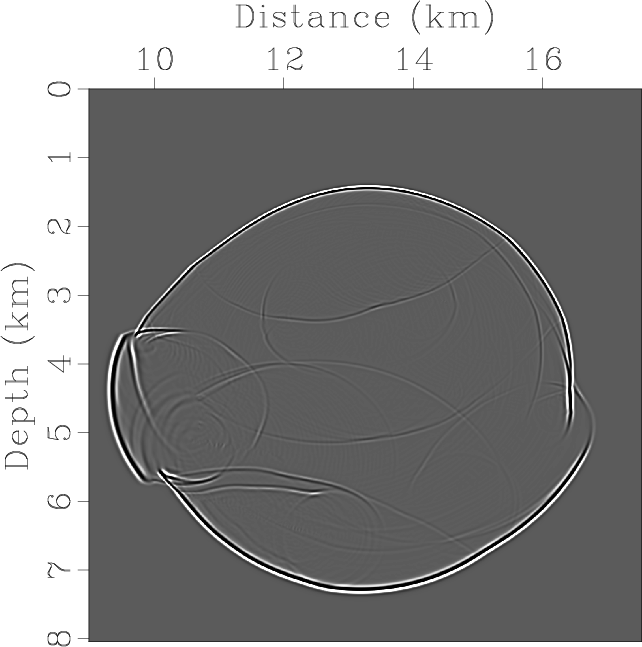
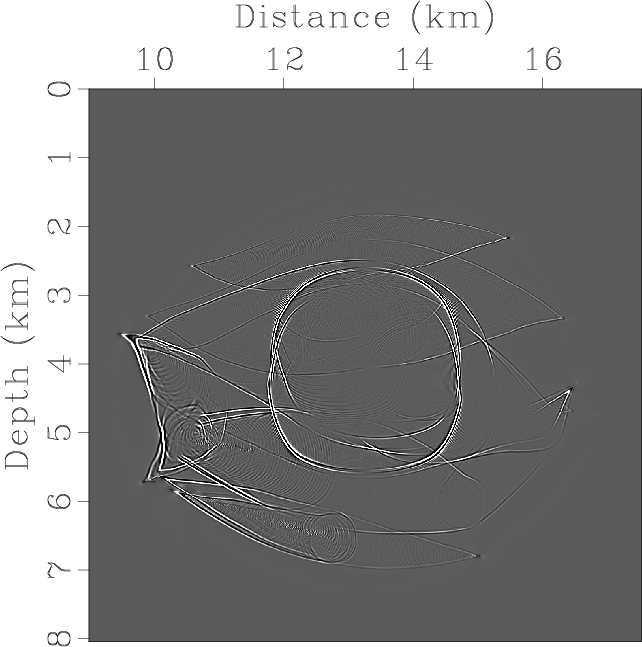
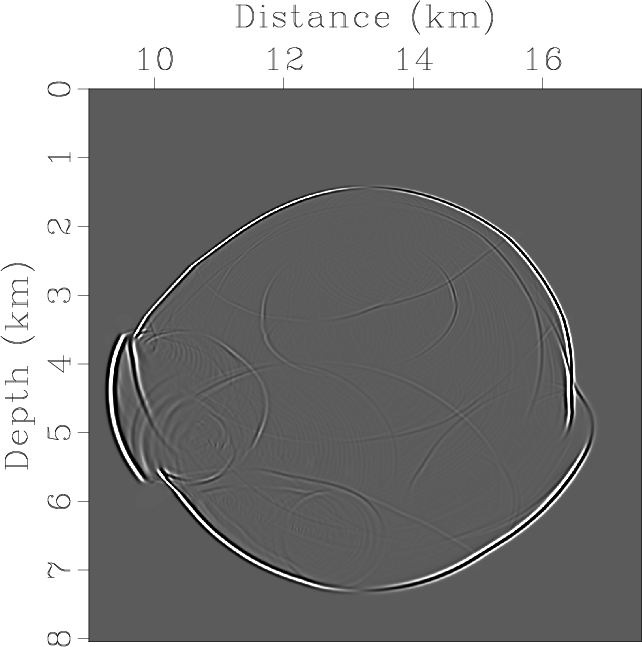
Figure 7 shows results of mode separation and vector decomposition, with the rank of about ![]() in both cases.
It took 133.0 seconds to decompose the operator matrixes for mode separation with rank
in both cases.
It took 133.0 seconds to decompose the operator matrixes for mode separation with rank ![]() , and 154.1 seconds to decompose the operator matrixes for vector decomposition with rank
, and 154.1 seconds to decompose the operator matrixes for vector decomposition with rank
![]() .
For one time step, it took about 2.2, 4.0, and 7.7 seconds to extrapolate, separate and decompose the elastic wavefields, repectively.
However, if nonstaionary spatial filtering is used to separate qP- and qSV-waves at every grid-point, it took about 2340.7 seconds
to calculate the filters in advance, and about 444.0 seconds with the truncated operator of size
.
For one time step, it took about 2.2, 4.0, and 7.7 seconds to extrapolate, separate and decompose the elastic wavefields, repectively.
However, if nonstaionary spatial filtering is used to separate qP- and qSV-waves at every grid-point, it took about 2340.7 seconds
to calculate the filters in advance, and about 444.0 seconds with the truncated operator of size
![]() at each time step during wavefield extrapolation.
This indicates that the mixed domain algorithms using low-rank approximation significantly improve the efficiency for wave mode separation.
Of course, larger amount of CPU time has been saved for vector decomposition by using the corresponding low-rank approximate algorithm.
at each time step during wavefield extrapolation.
This indicates that the mixed domain algorithms using low-rank approximation significantly improve the efficiency for wave mode separation.
Of course, larger amount of CPU time has been saved for vector decomposition by using the corresponding low-rank approximate algorithm.
|
|---|
|
vp-hess,epsilon-hess,delta-hess
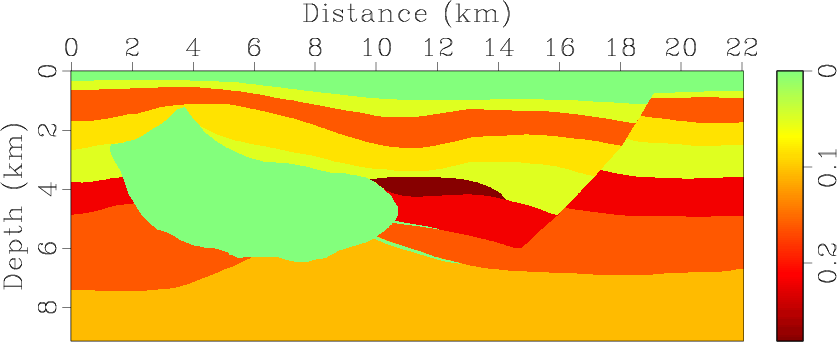
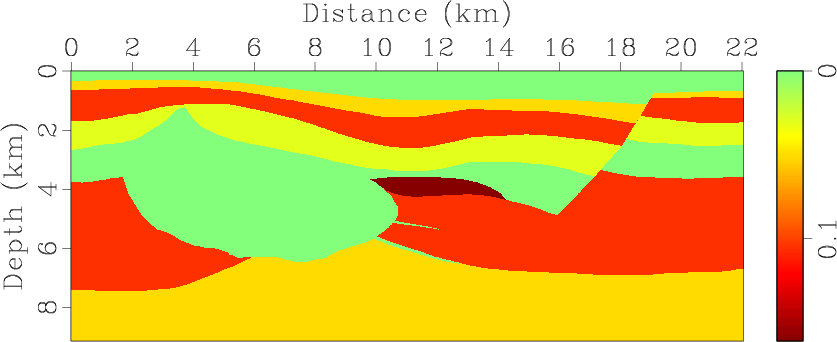
Figure 7. Hess VTI model with parameters of (a) vertical P-wave velocity, Thomsen coefficients (b) |
|
|
|
|---|
|
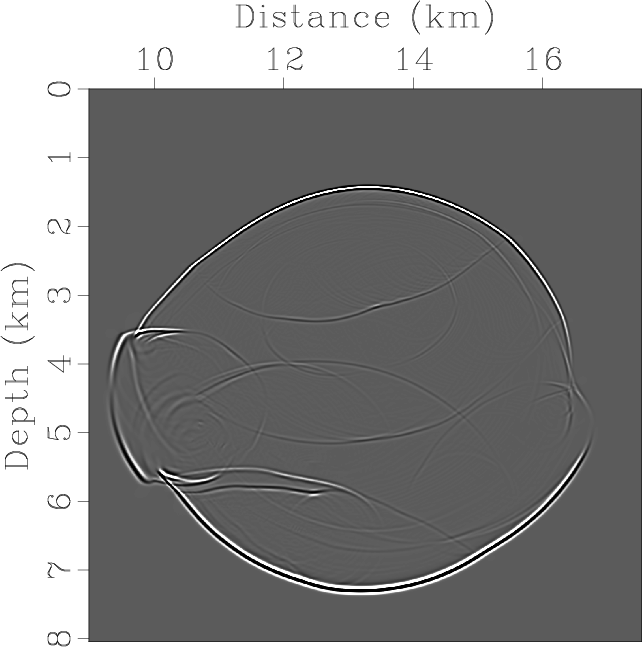
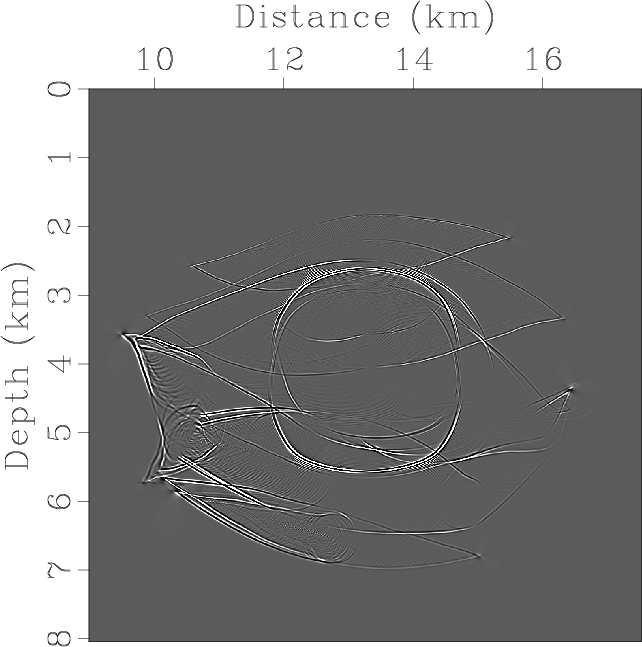
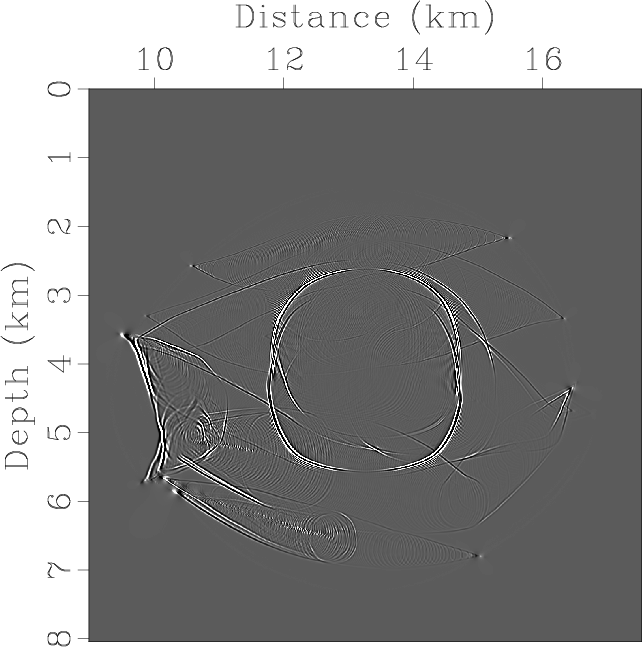
Elasticx,Elasticz,ElasticSepP,ElasticSepSV,ElasticPx,ElasticPz,ElasticSVx,ElasticSVz
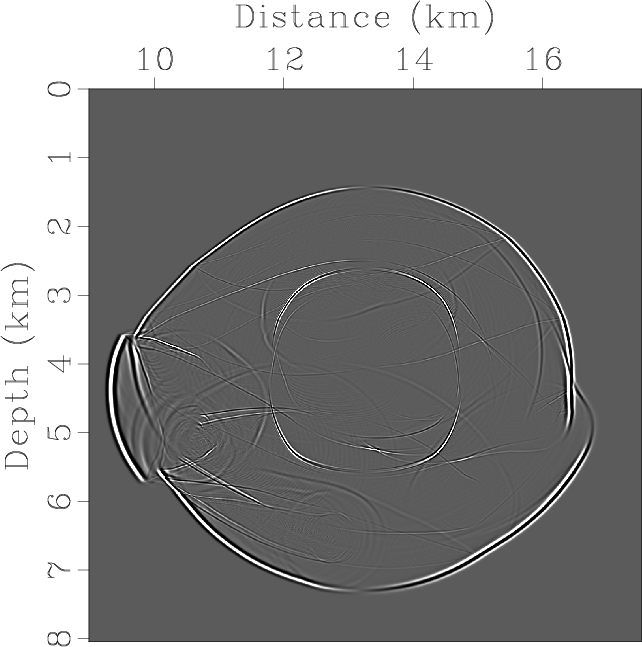
Figure 8. Elastic wave mode separation and vector decomposition in the Hess VTI model: (a) x- and (b) z-components of the synthetic elastic displacement wavefields at 1.1s; (c) and (d) are the separated scalar qP- and qSV-wave fields; (e) x- and (f) z-components of vector qP-wave fields; (g) x- and (h) z-components of vector qSV-wave fields. |
|
|
|
|
|
|
Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |