|
|
|
|
Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |
For comparison, we only change the second layer to a TTI medium with a tilt angle
![]() and azimuth
and azimuth
![]() (other paramters continue to use).
Figure 6 displays the corresponding elastic wavefields and their mode separation results.
It took 4087.8, 4280.8 and 206.2 seconds to construct the separated forms of the mode separation matrixes for qP-, qSV- and SH-waves, respectively.
For one time step, it took 101.0 seconds to extrapolate the elastic wavefield, and 15.2 and 15.8 seconds to separate qP- and qSV-wave modes with
the rank
(other paramters continue to use).
Figure 6 displays the corresponding elastic wavefields and their mode separation results.
It took 4087.8, 4280.8 and 206.2 seconds to construct the separated forms of the mode separation matrixes for qP-, qSV- and SH-waves, respectively.
For one time step, it took 101.0 seconds to extrapolate the elastic wavefield, and 15.2 and 15.8 seconds to separate qP- and qSV-wave modes with
the rank ![]() . It took 14.1 seconds to separate SH-wave with the rank
. It took 14.1 seconds to separate SH-wave with the rank ![]() .
As we observed, the most time-consuming task here is to construct the separated forms of the mode separation matrixes.
More CPU time is required to separate SH-wave in 3D TTI media as well.
.
As we observed, the most time-consuming task here is to construct the separated forms of the mode separation matrixes.
More CPU time is required to separate SH-wave in 3D TTI media as well.


|
|---|
|
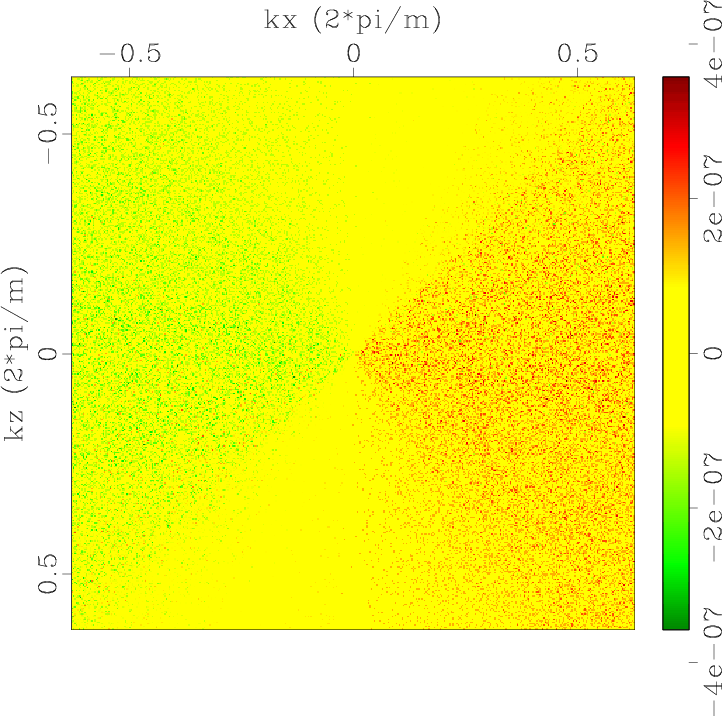
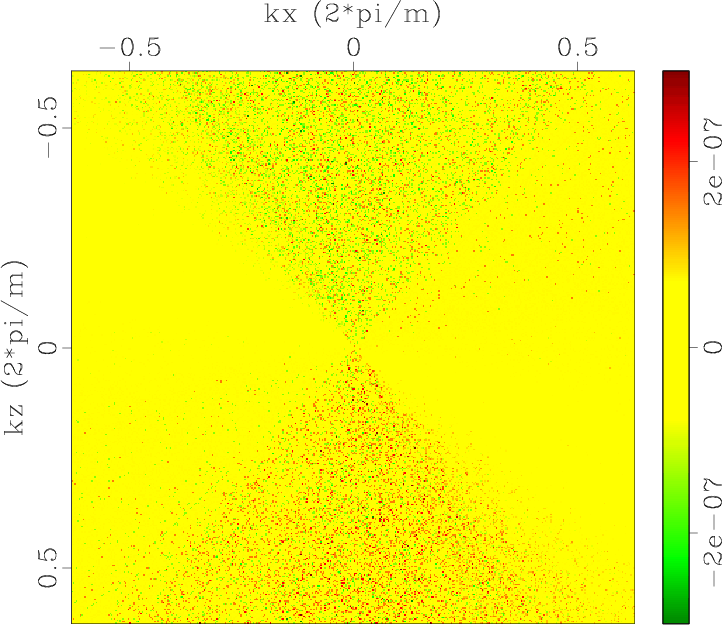
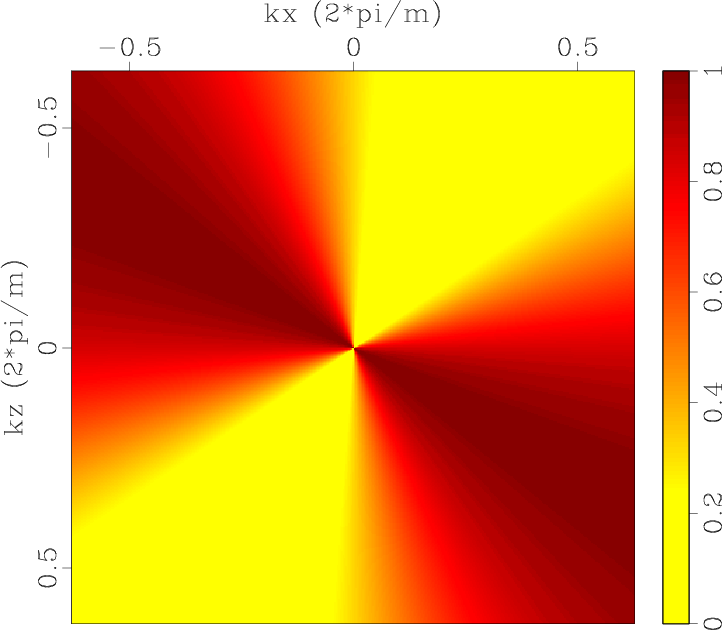
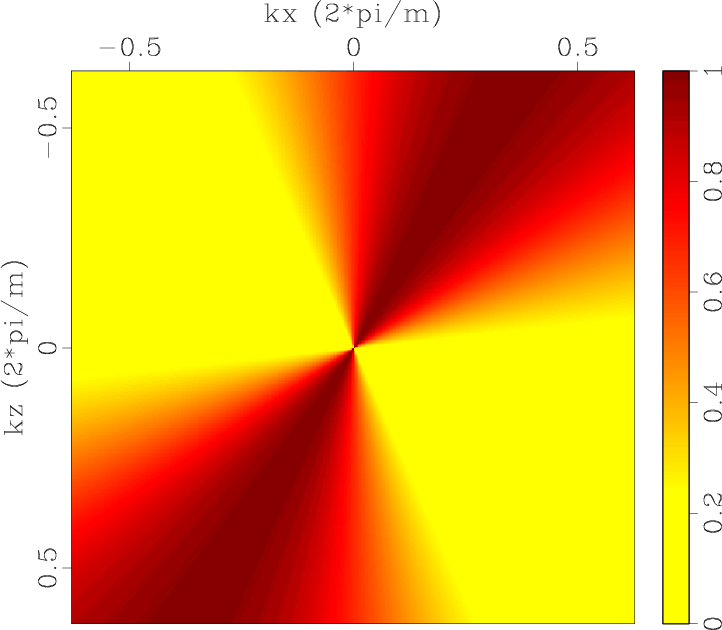
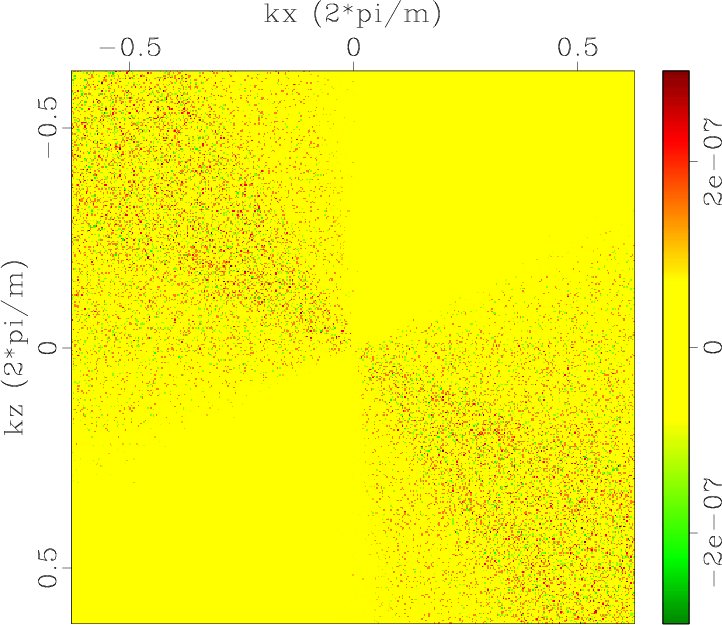
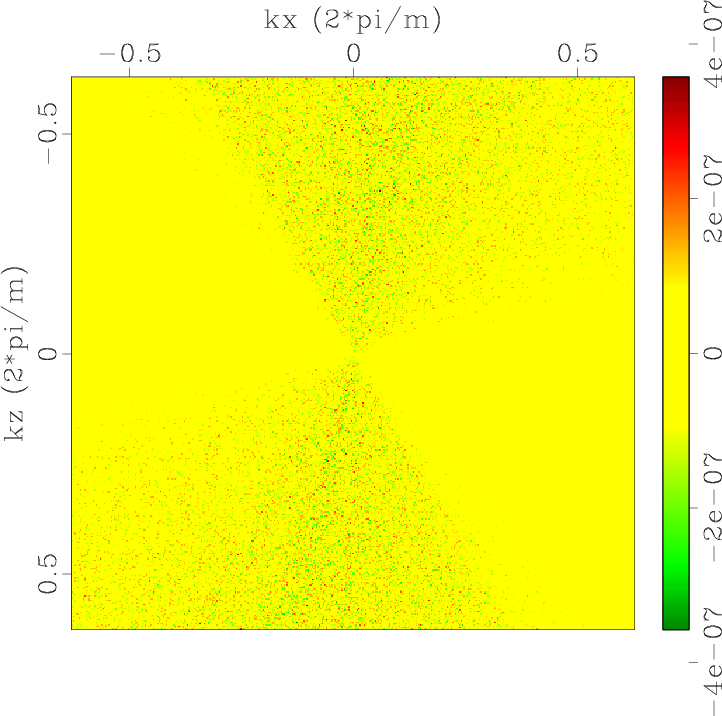
Polxp1,Polzp1,Polxp2,Polzp2,Errpolxp1,Errpolzp1,Errpolxp2,Errpolzp2
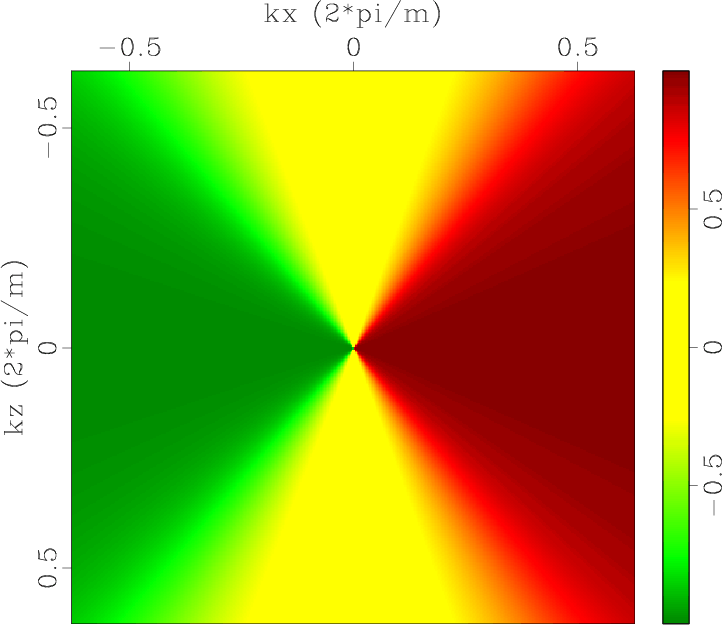
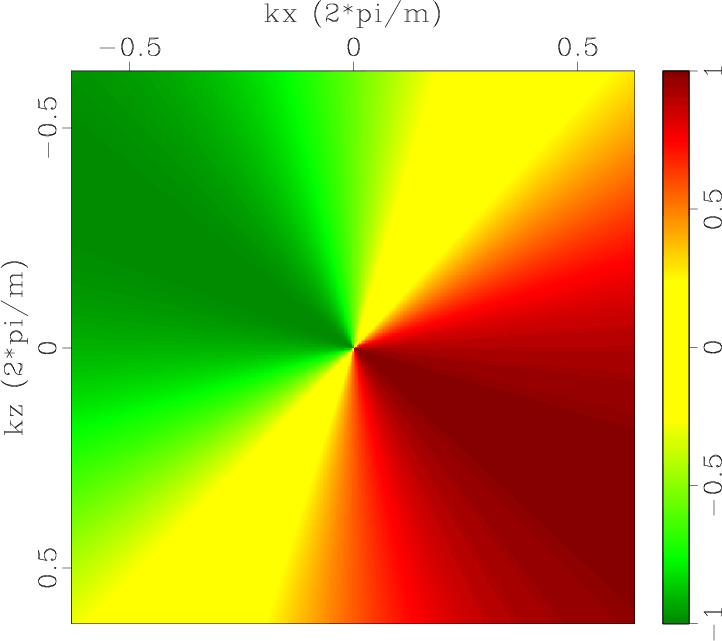
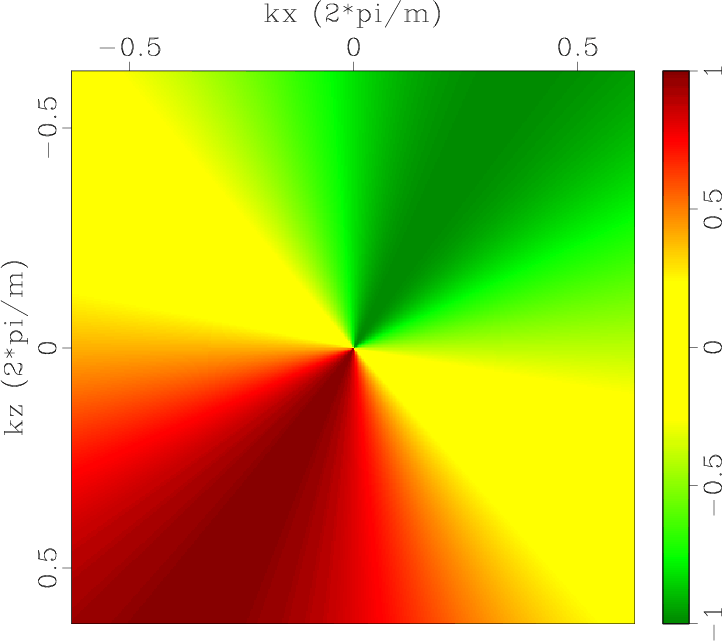
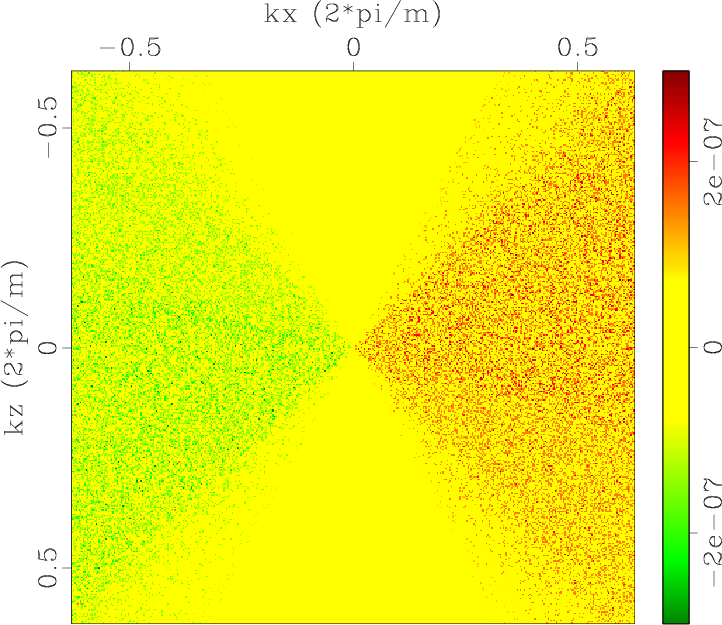
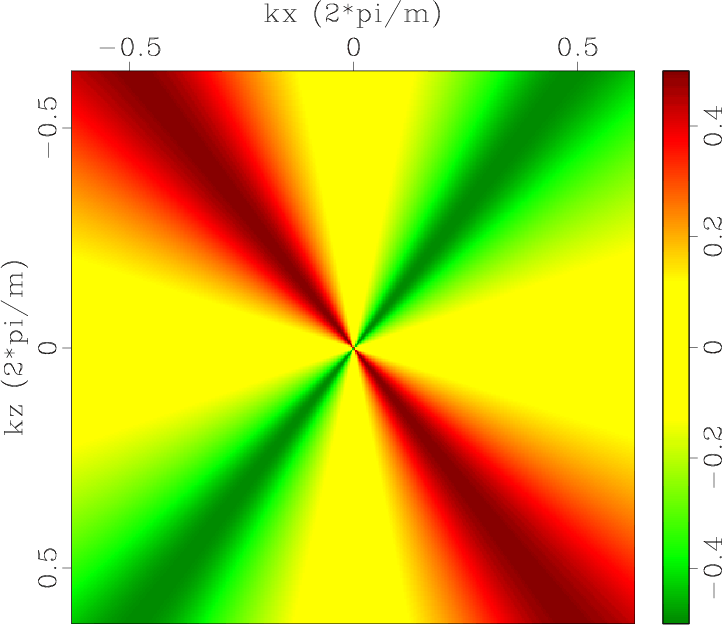
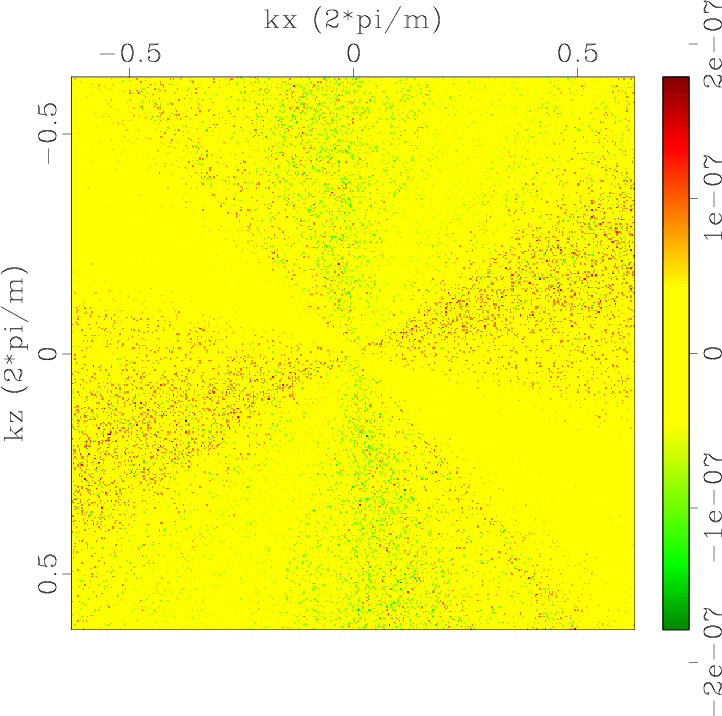
Figure 1. Low-rank approximate mode separators of qP-wave in a 2D two-layer TI model: (a) |
|
|




|
|---|
|
ElasticxInterf,ElasticzInterf,ElasticSepPInterf,ElasticSepSVInterf
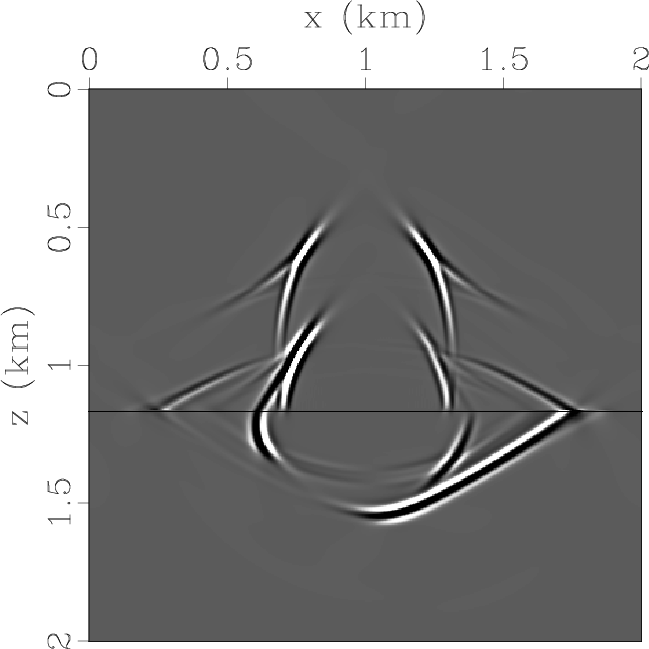
Figure 2. Elastic wave mode separation in the two-layer TI model: (a) x- and (b) z-components of the synthetic elastic displacement wavefields synthesized at 0.3s; (c) and (d) are the separated scalar qP- and qSV-wave fields using low-rank approximation. |
|
|

|
|---|
|
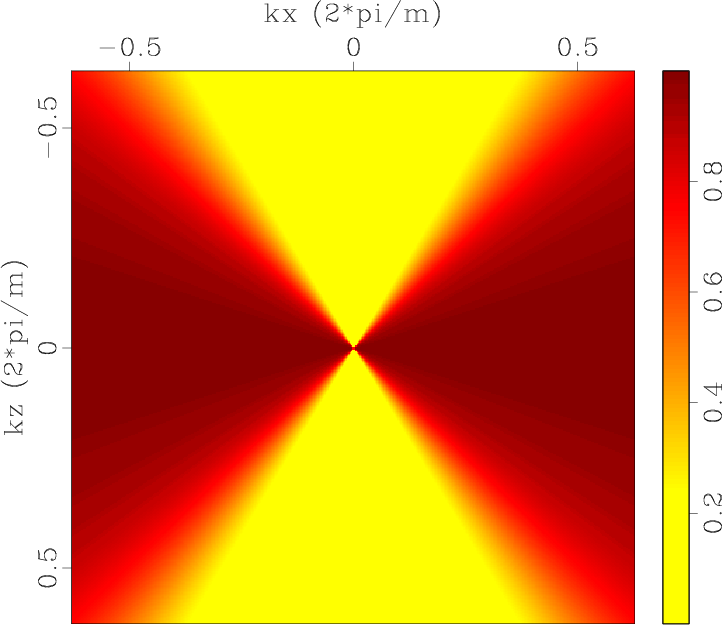
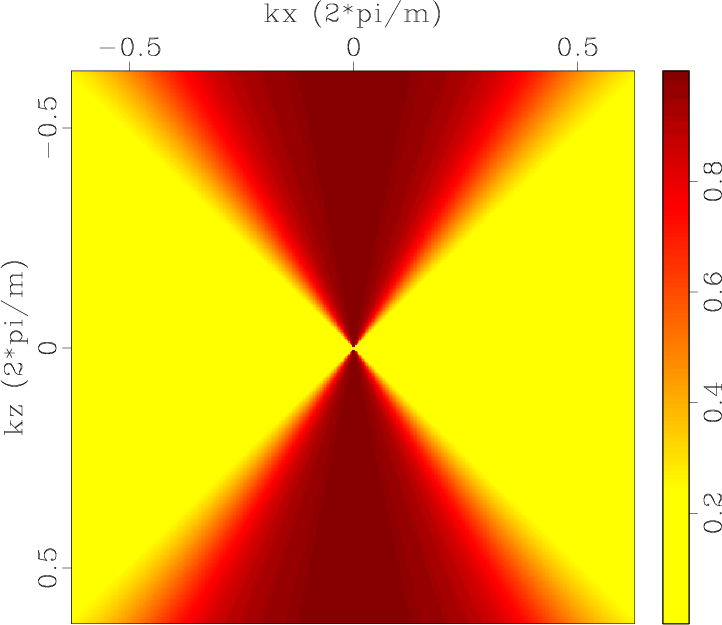
Decompxp1,Decompzp1,Decompxzp1,Errdecxp1,Errdeczp1,Errdecxzp1,Decompxp2,Decompzp2,Decompxzp2,Errdecxp2,Errdeczp2,Errdecxzp2
Figure 3. Low-rank approximate vector decomposition operators of qP-wave in the 2D two-layer TI model: (a) |
|
|



|
|---|
|
ElasticPxInterf,ElasticPzInterf,ElasticSVxInterf,ElasticSVzInterf
Figure 4. Elastic wave vector decomposition in the two-layer VTI/VTI model: (a) x- and (b) z-components of vector qP-wave fields; (c) x- and (d) z-components of vector qSV-wave fields. |
|
|
|
|---|
|
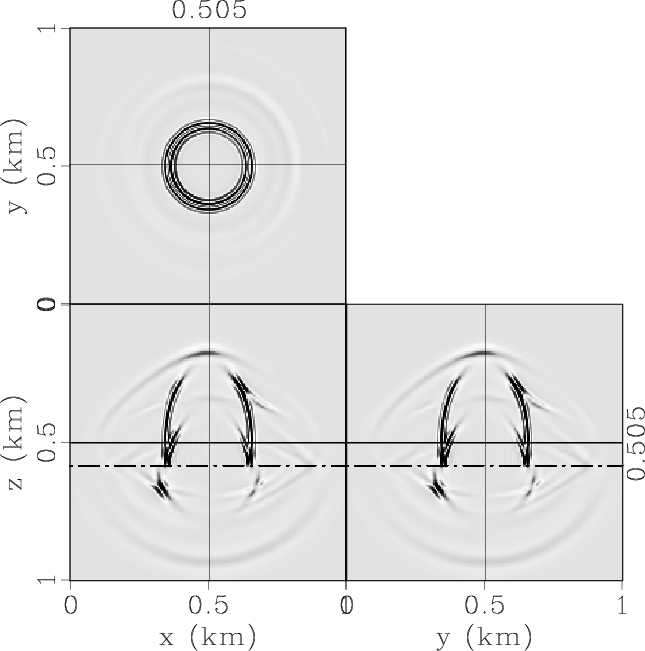
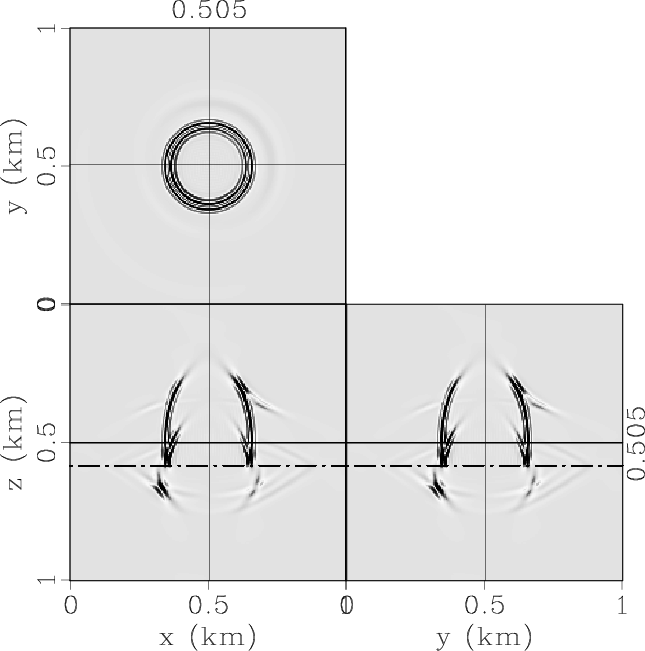
ElasticxInterf,ElasticyInterf,ElasticzInterf,ElasticPInterf,ElasticSVInterf,ElasticSHInterf
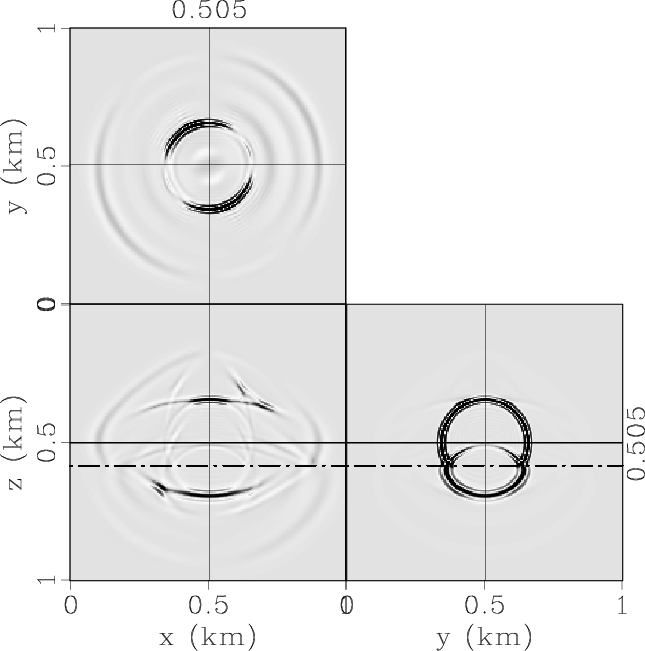
Figure 5. Elastic wave mode separation in the 3D two-layer VTI model: (a) x-, (b) y- and (c) z-components of the synthetic elastic displacement wavefields synthesized at 0.17s; (d) qP-, (e) qSV- and (e) SH-wave fields separated from the elastic wavefields. |
|
|
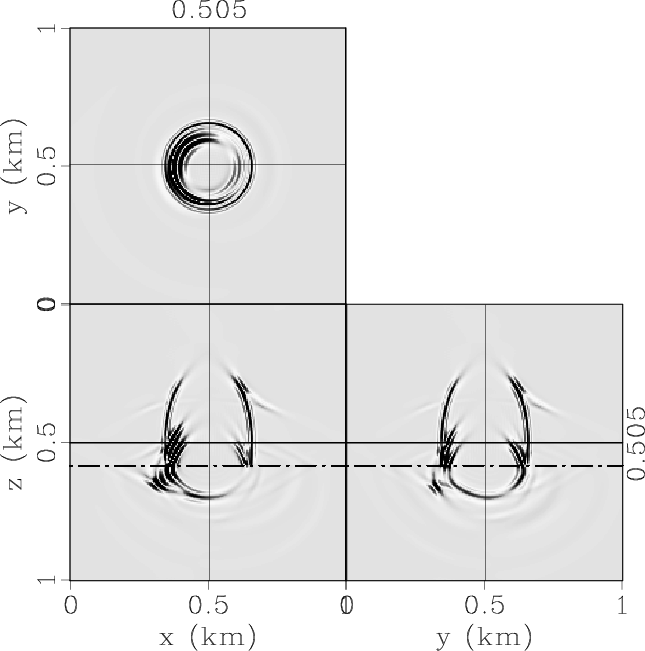
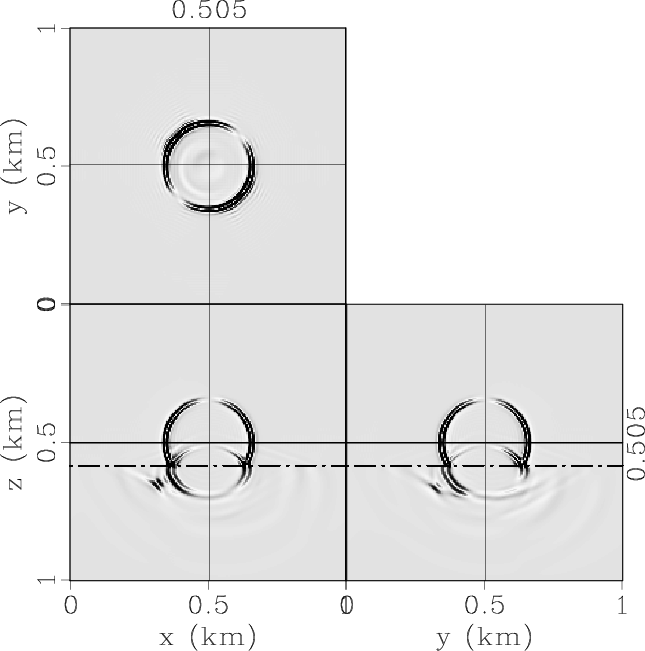
|
|---|
|
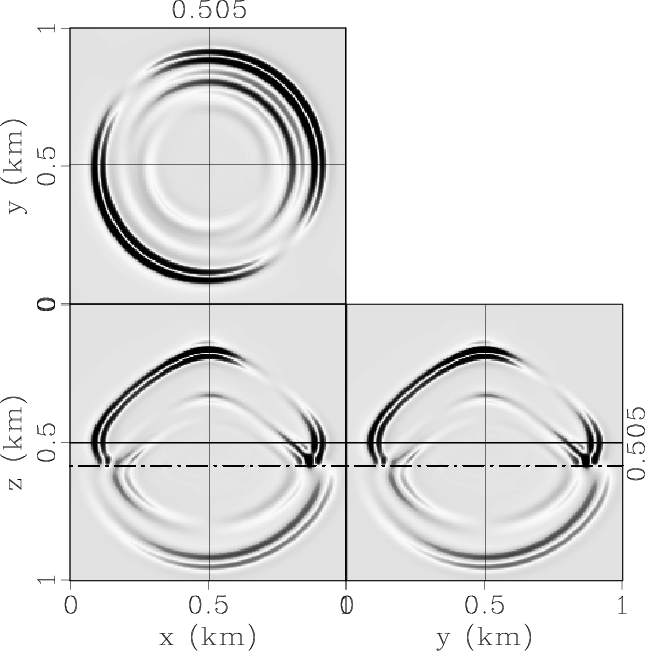
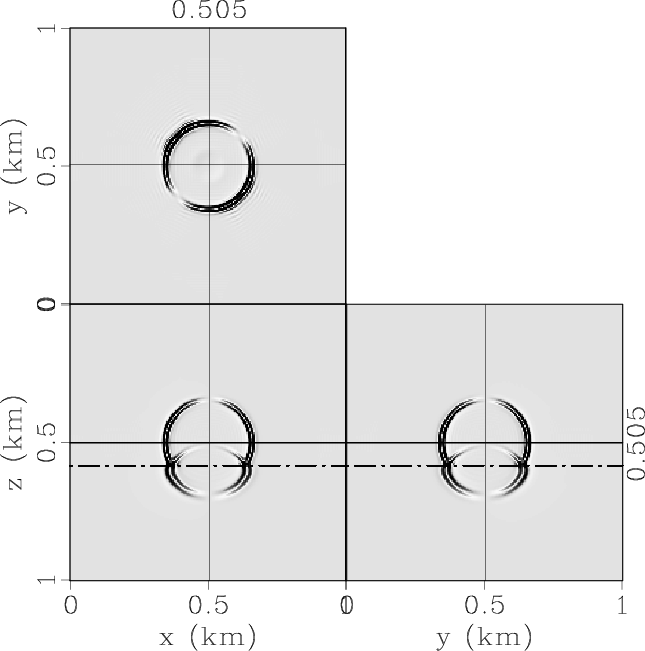
ElasticxInterf,ElasticyInterf,ElasticzInterf,ElasticPInterf,ElasticSVInterf,ElasticSHInterf
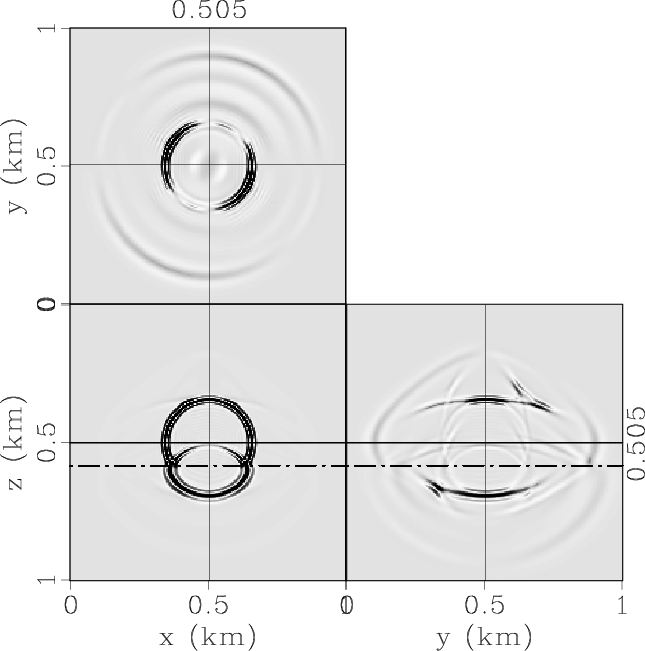
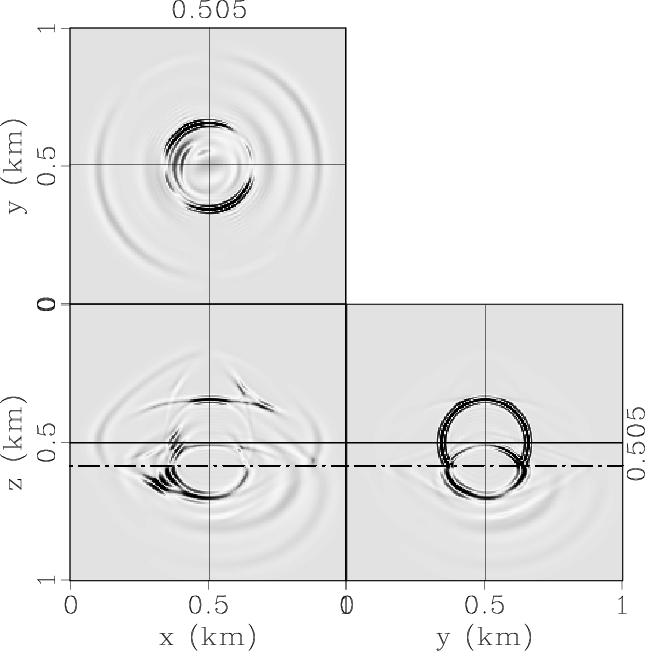
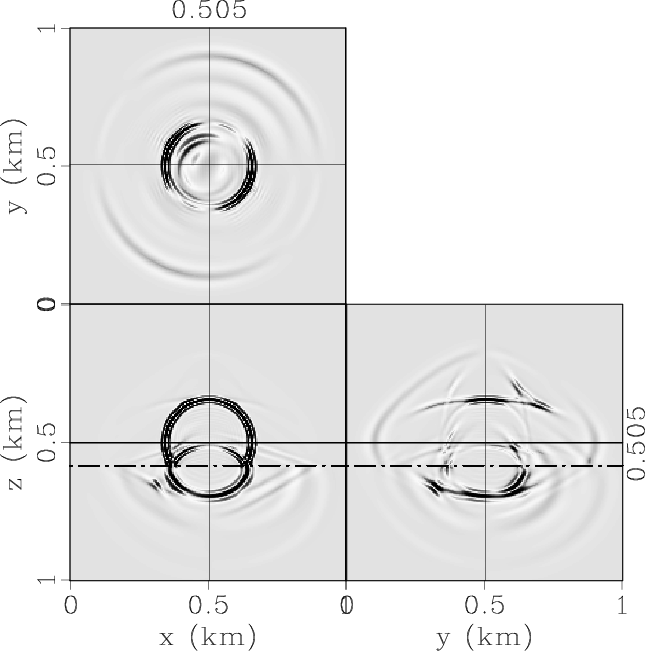
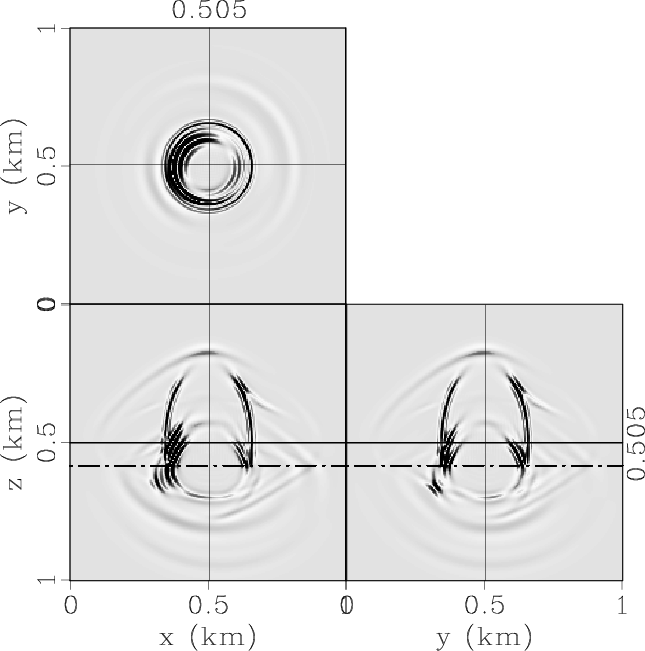
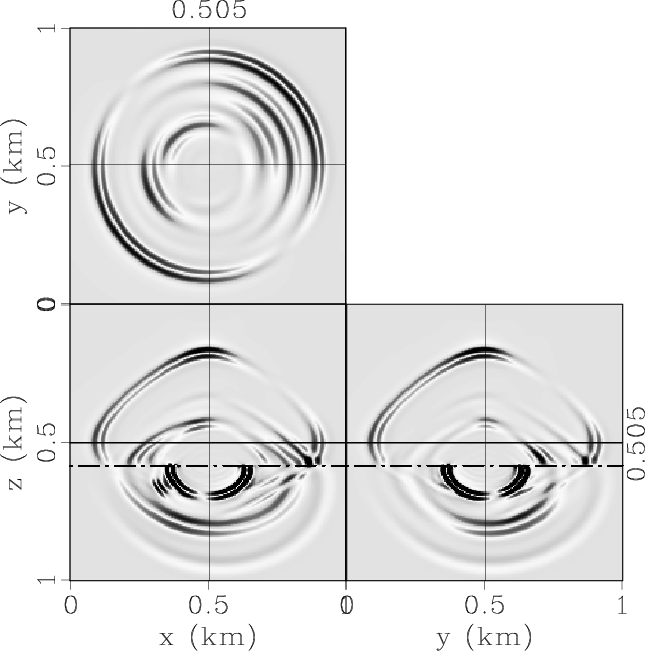
Figure 6. Elastic wave mode separation in the 3D two-layer VTI/TTI model: (a) x-, (b) y- and (c) z-components of the synthetic elastic displacement wavefields synthesized at 0.17s; (d) qP-, (e) qSV- and (e) SH-wave fields separated from the elastic wavefields. |
|
|
|
|
|
|
Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |