|
|
|
|
Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |
Then we investigate the effect of the relative accuracy requirement on wave mode separation.
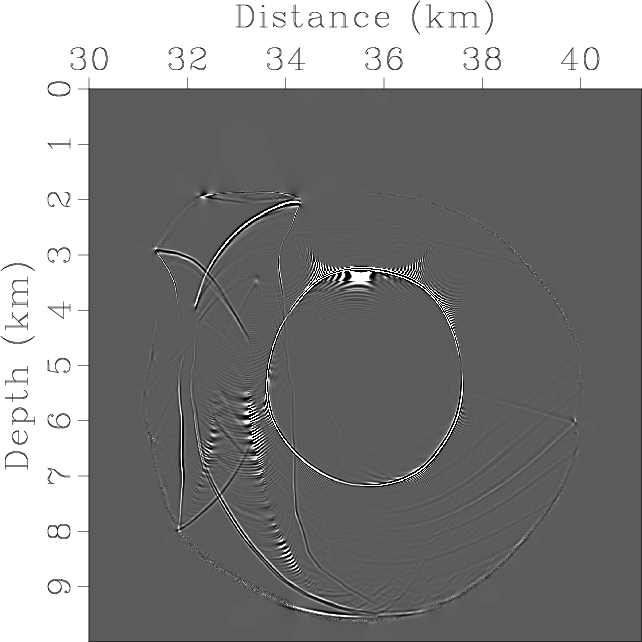
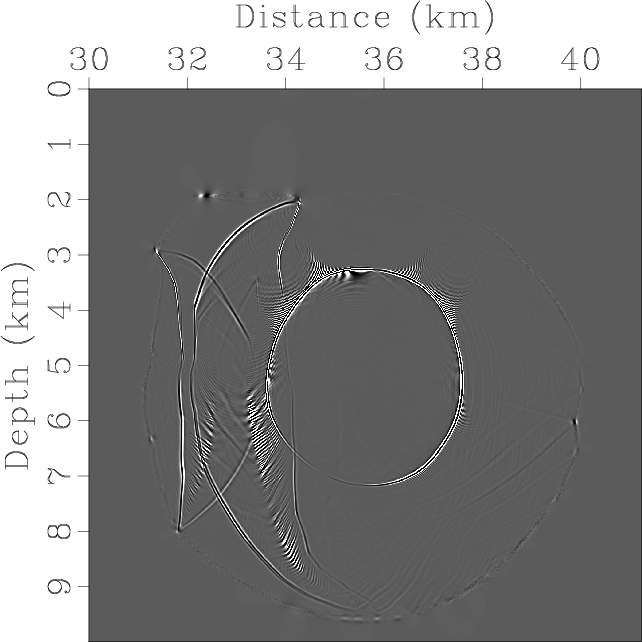
Figure 11 demonstrates the separated P- and qSV-wave fields, and their variations when we relax the approximation level
from ![]() to
to ![]() .
It took 174.0 seconds to decompose the operator matrixes for mode separation with rank
.
It took 174.0 seconds to decompose the operator matrixes for mode separation with rank
![]() , and
345.5 seconds to decompose the operator matrixes for vector decomposition with rank
, and
345.5 seconds to decompose the operator matrixes for vector decomposition with rank
![]() .
And it took 8.0 and 14.9 seconds to separate and decompose the elastic wavefields, repectively.
The results are acceptable although more errors are introduced in the separated wavefields
when we turn down the relative accuracy requirement.
.
And it took 8.0 and 14.9 seconds to separate and decompose the elastic wavefields, repectively.
The results are acceptable although more errors are introduced in the separated wavefields
when we turn down the relative accuracy requirement.
To further analysize the rough relationship of rank ![]() with the model complexity, we smooth the BP TTI model
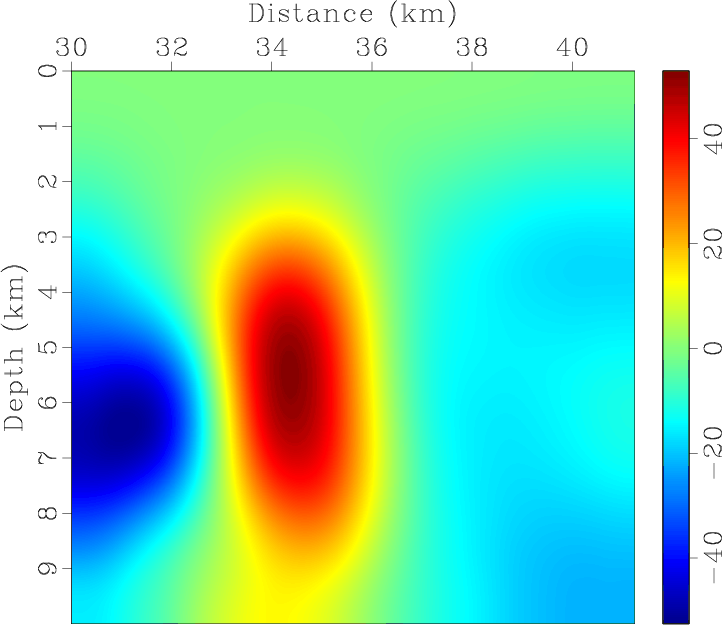
by applying a 2D triangle smoothing operator with the radius of 1875m on both x- and z-axes (Figure 12).
To maintain the range of the tilt angles, we first double the values of the original model and then apply the smoothing operation
for this parameter.
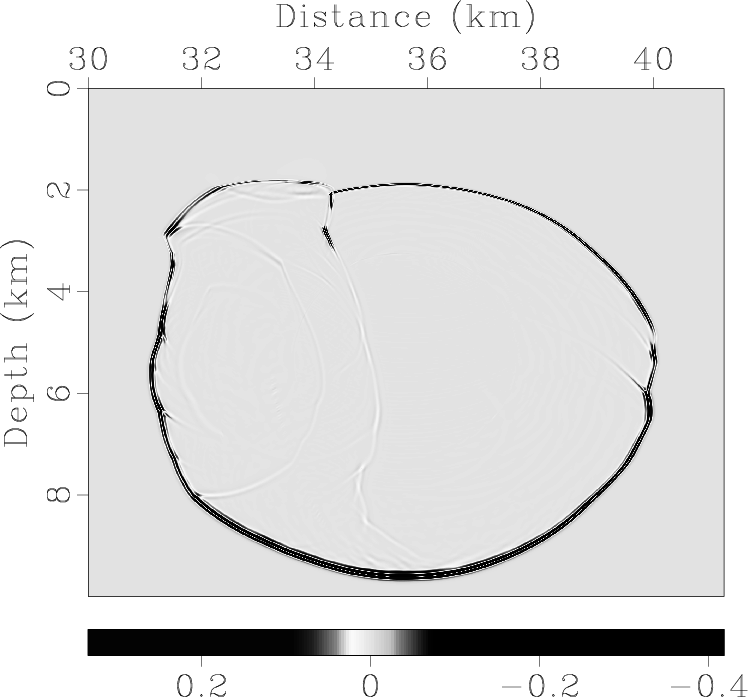
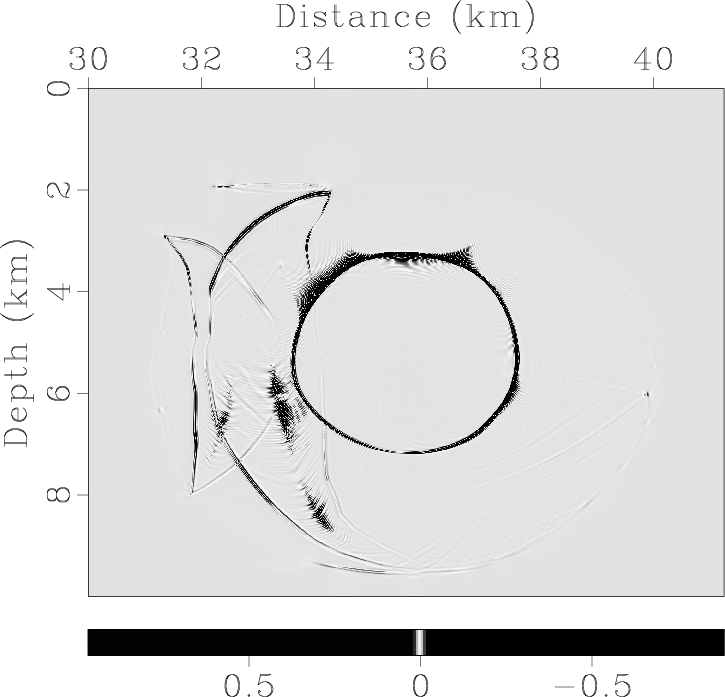
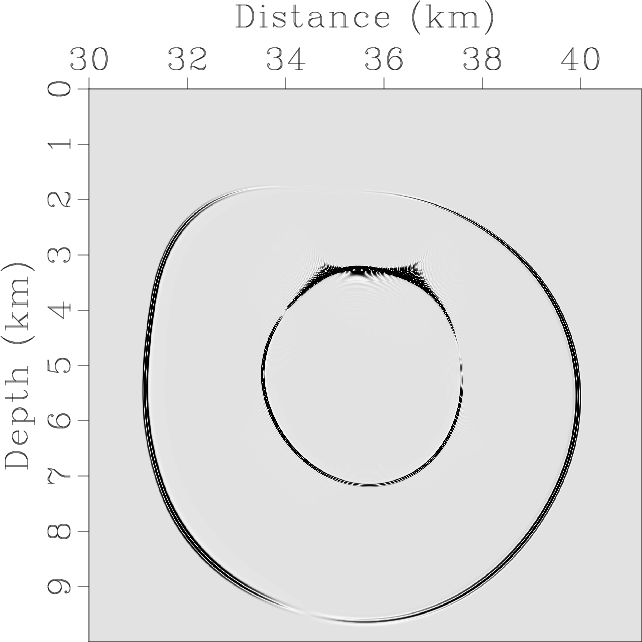
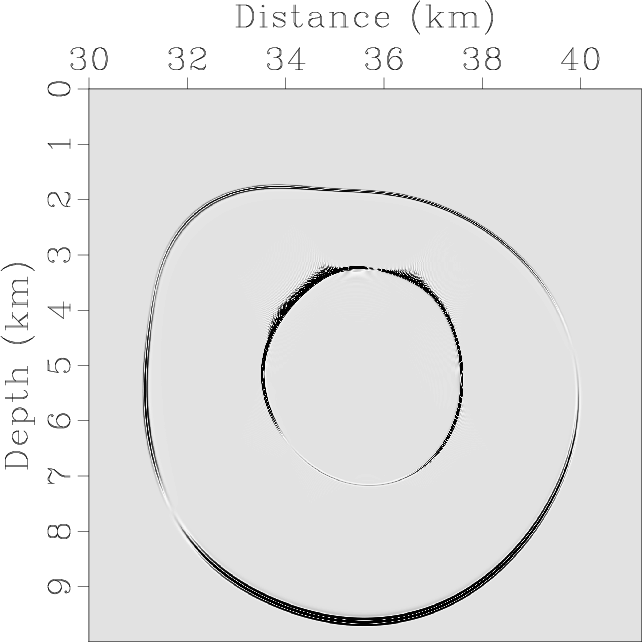
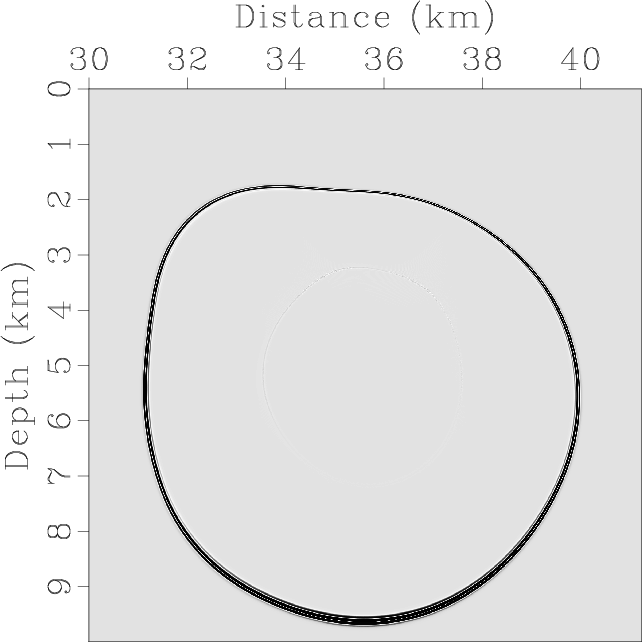
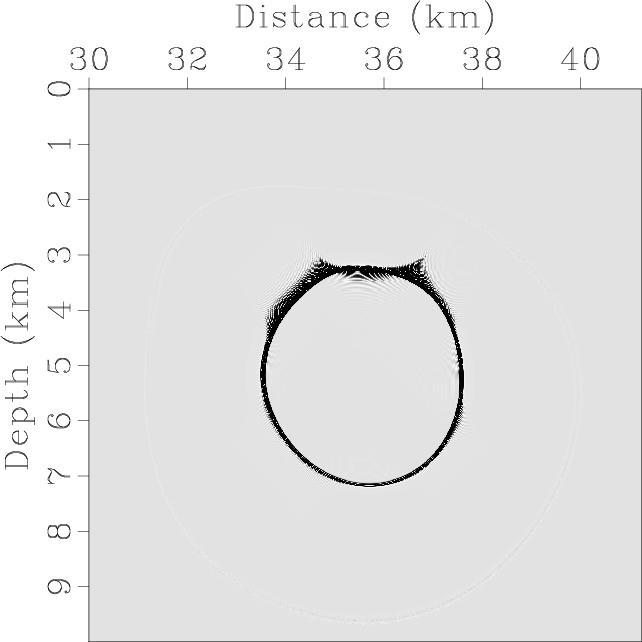
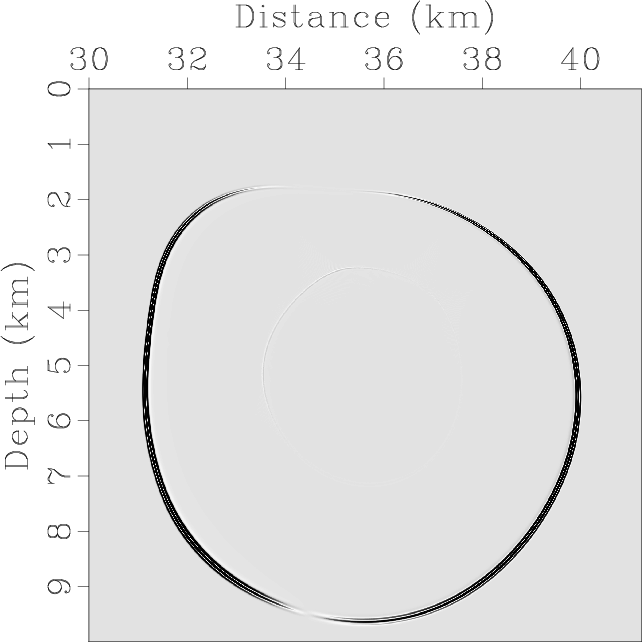
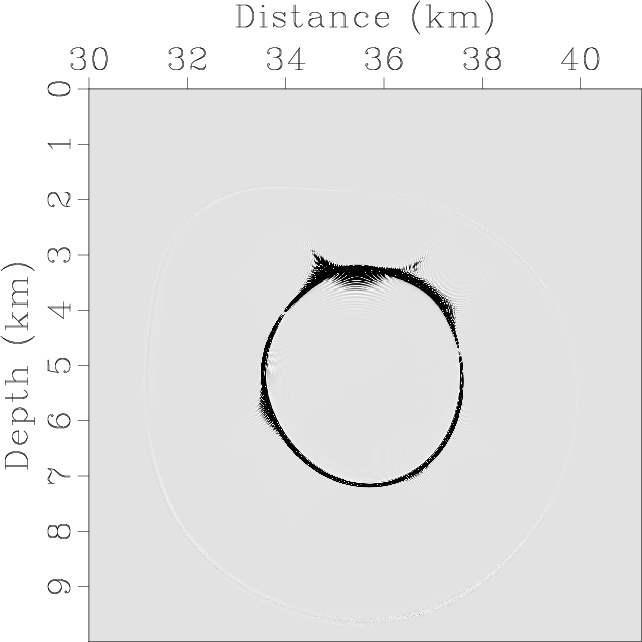
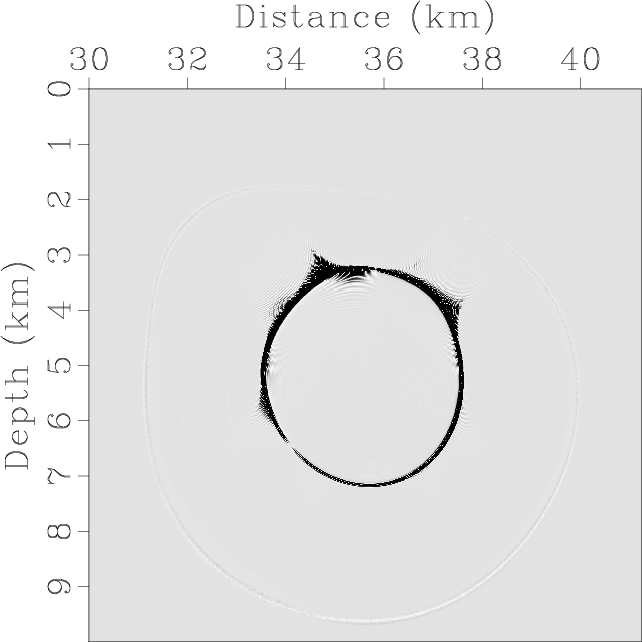
Figure 13 demonstrates the synthetic elastic wavefields and the mode separation and vector decomposition results.
In this case, it took 207.0 seconds to decompose the operator matrixes for mode separation with rank
with the model complexity, we smooth the BP TTI model
by applying a 2D triangle smoothing operator with the radius of 1875m on both x- and z-axes (Figure 12).
To maintain the range of the tilt angles, we first double the values of the original model and then apply the smoothing operation
for this parameter.
Figure 13 demonstrates the synthetic elastic wavefields and the mode separation and vector decomposition results.
In this case, it took 207.0 seconds to decompose the operator matrixes for mode separation with rank
![]() , and
310.2 seconds to decompose the operator matrixes for vector decomposition with rank
, and
310.2 seconds to decompose the operator matrixes for vector decomposition with rank
![]() .
It took 15.0 and 29.4 seconds to separate and decompose the elastic wavefields, repectively.
We observe that the ranks further decrease to about 12 if we double the smoothing radius to 3750m.
For homogeneous TI medium, the ranks automatically decrease to 1.
We obtain accurate mode separation and decomposition of the isotropic and elastic wavefields
at negligible computational cost with rank
.
It took 15.0 and 29.4 seconds to separate and decompose the elastic wavefields, repectively.
We observe that the ranks further decrease to about 12 if we double the smoothing radius to 3750m.
For homogeneous TI medium, the ranks automatically decrease to 1.
We obtain accurate mode separation and decomposition of the isotropic and elastic wavefields
at negligible computational cost with rank ![]() ,
if
,
if ![]() ,
, ![]() and
and ![]() are all set as
are all set as ![]() in the models.
in the models.

|
|---|
|
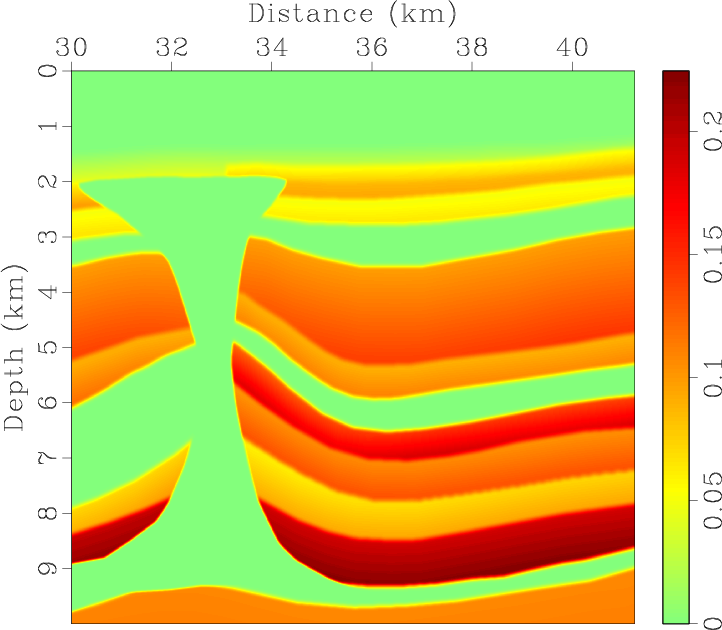
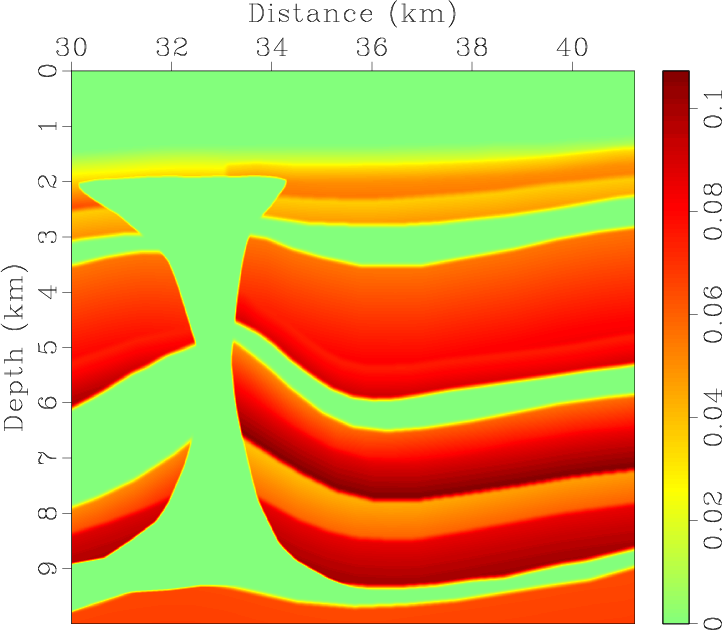
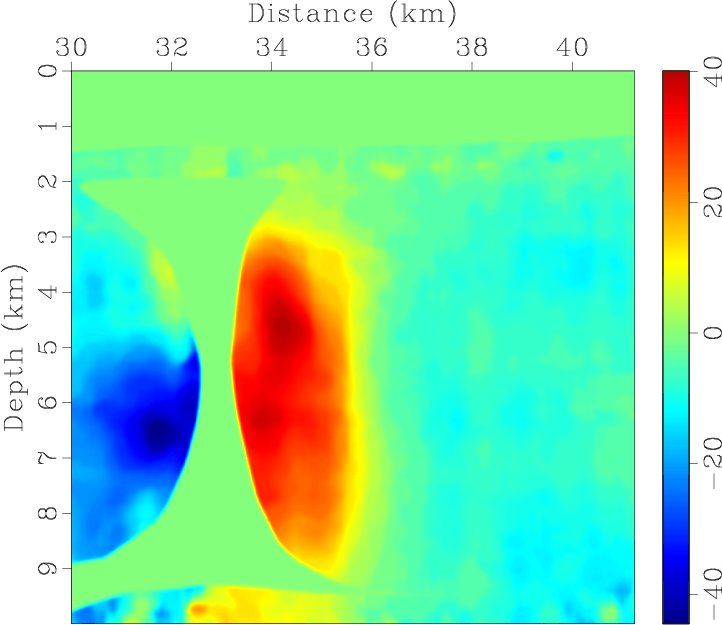
vp0,epsi,del,the
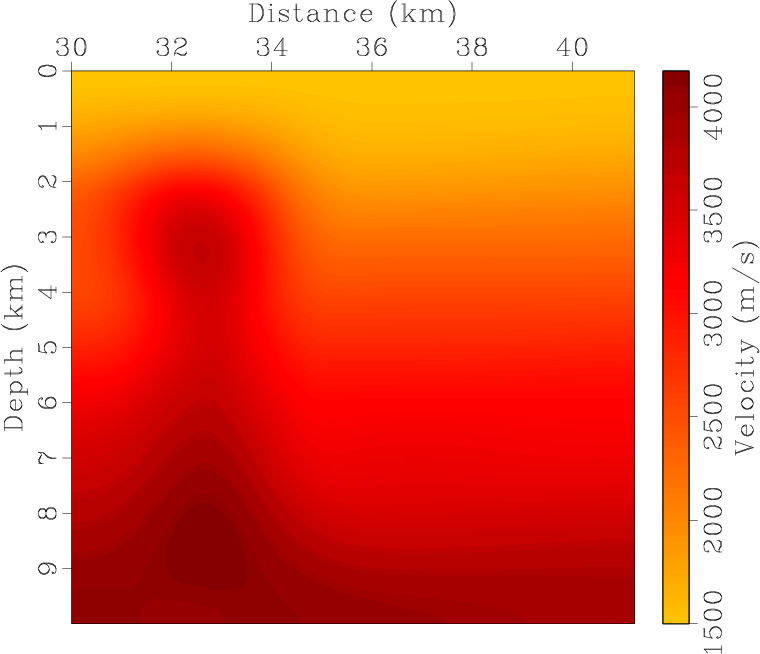
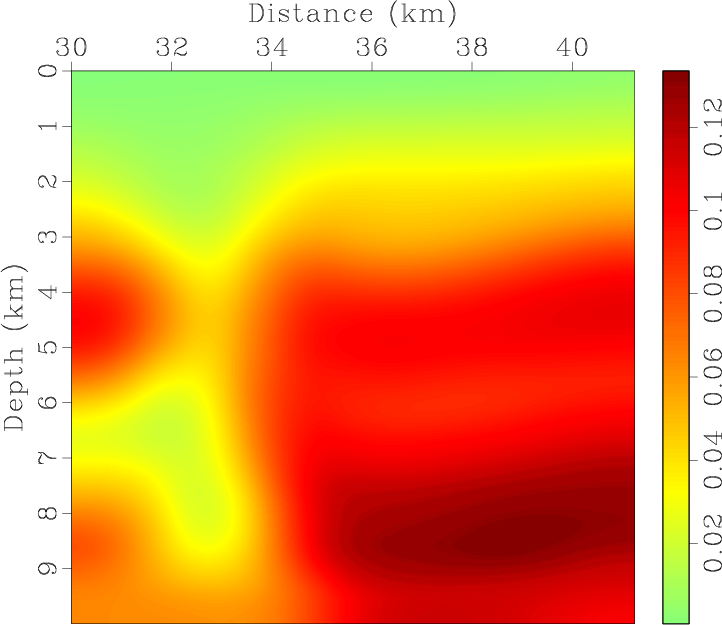
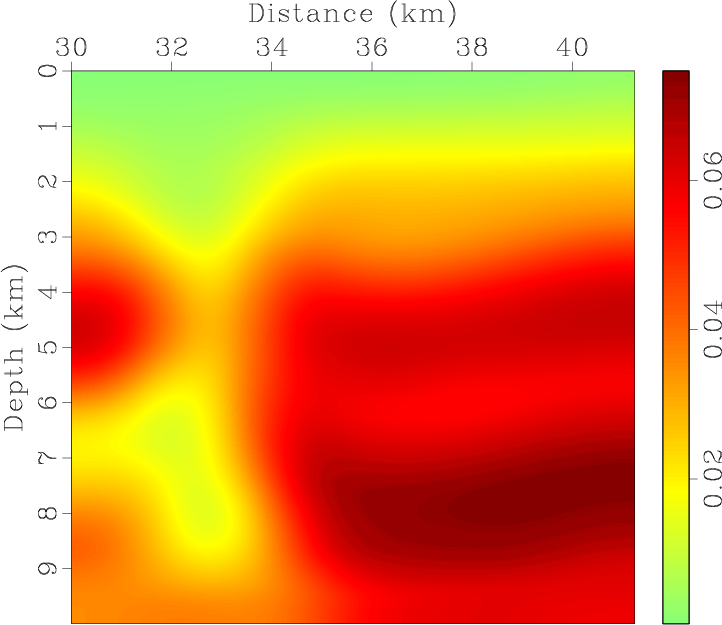
Figure 9. BP 2007 TTI model with parameters of (a) vertical P-wave velocity, Thomsen coefficients (b) |
|
|

|
|---|
|
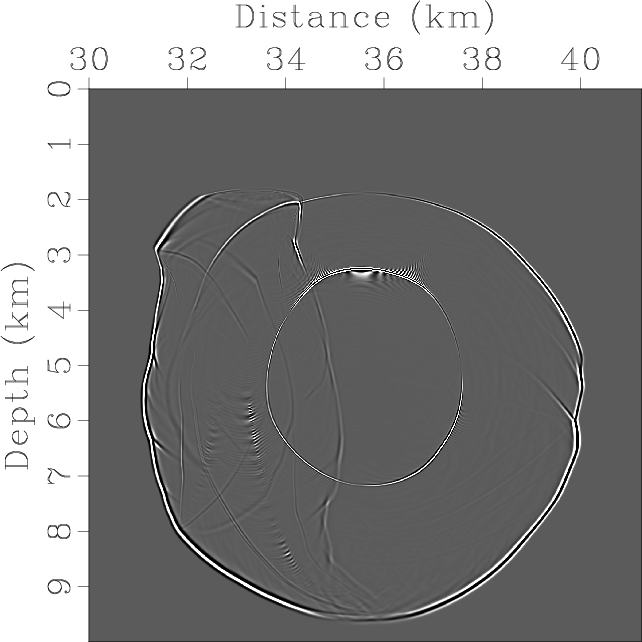
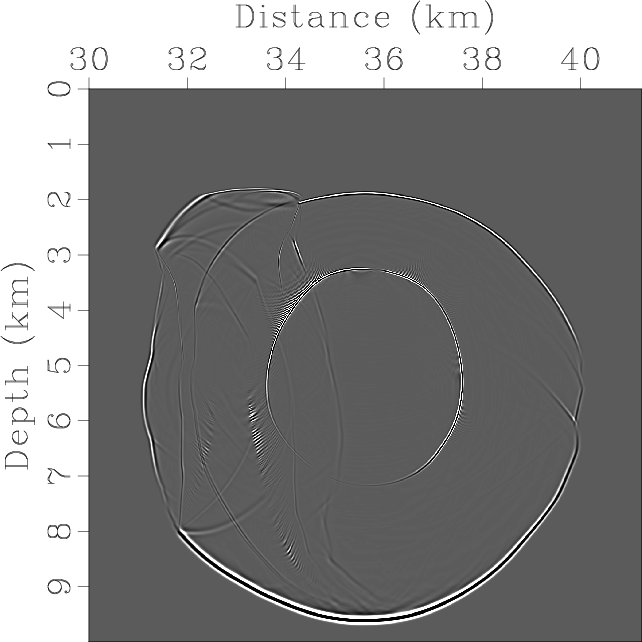
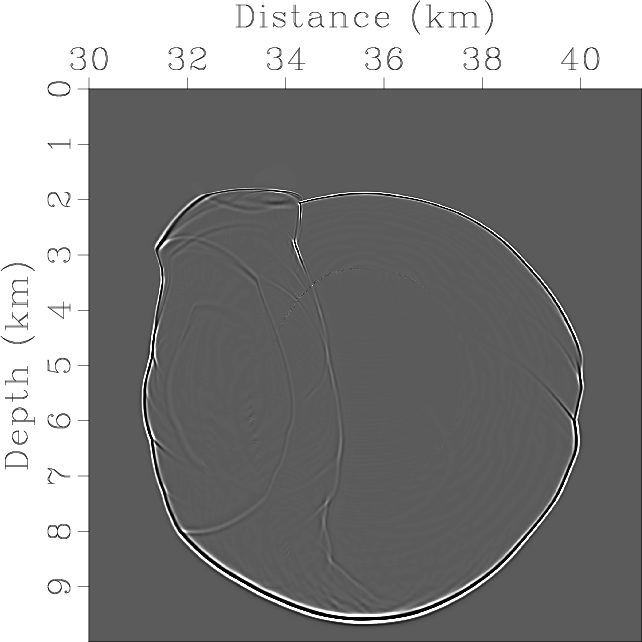
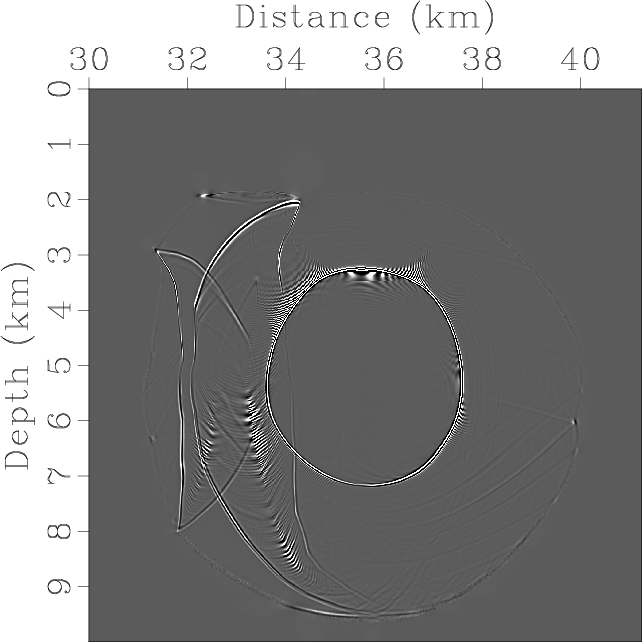
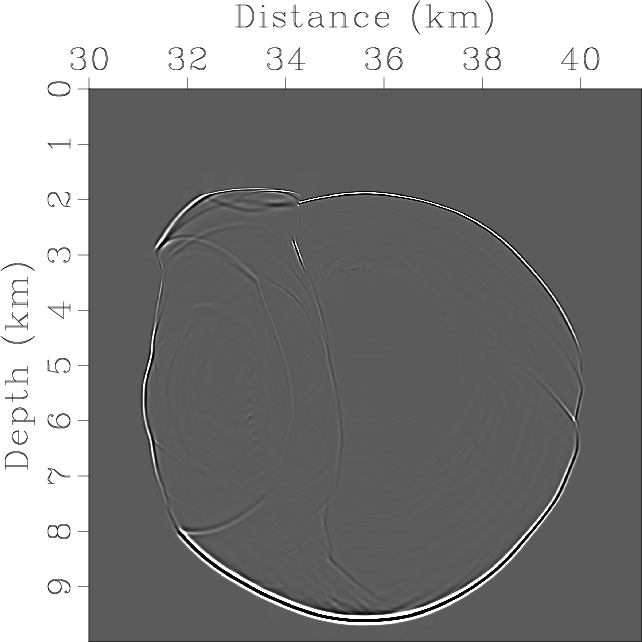
Elasticx,Elasticz,ElasticSepP,ElasticSepSV,ElasticPx,ElasticPz,ElasticSVx,ElasticSVz
Figure 10. Mode separation and vector decomposition using low-rank approximate algorithms in the BP 2007 TTI model: (a) x- and (b) z-components of the synthetic elastic displacement wavefields at 1.4s; (c) and (d) are the separated scalar qP- and qSV-wave fields; (e) x- and (f) z-components of vector qP-wave fields; (g) x- and (h) z-components of vector qSV-wave fields. |
|
|

|
|---|
|
ElasticSepP3,ElasticSepSV3,ElasticSepP6vs3Dif,ElasticSepSV6vs3Dif
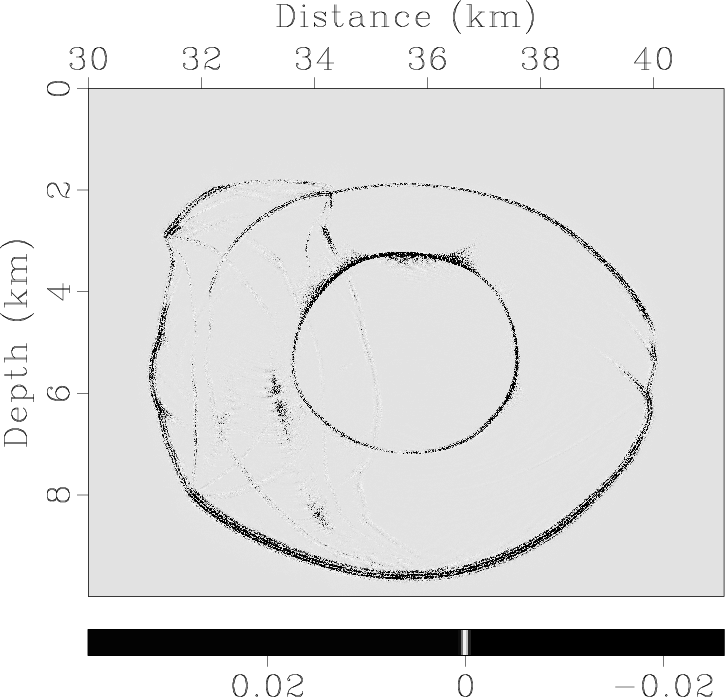
Figure 11. Elastic wave mode separation using low-rank approximation with relaxed accuracy requirements: Separated (a) qP- and (b) qSV-wave fields at the error level of |
|
|
|
|---|
|
vp0,epsi,del,the
Figure 12. Smoothed BP 2007 TTI model with parameters of (a) vertical P-wave velocity, Thomsen coefficients (b) |
|
|

|
|---|
|
Elasticx,Elasticz,ElasticSepP,ElasticSepSV,ElasticPx,ElasticPz,ElasticSVx,ElasticSVz
Figure 13. Mode separation and vector decomposition using low-rank approximate algorithms in the BP 2007 TTI model: (a) x- and (b) z-components of the synthetic elastic displacement wavefields at 1.4s; (c) and (d) are the separated scalar qP- and qSV-wave fields; (e) x- and (f) z-components of vector qP-wave fields; (g) x- and (h) z-components of vector qSV-wave fields. |
|
|
|
|
|
|
Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media |