|
|
|
|
Least-squares non-stationary triangle smoothing |
Next: Smoothing Filters and Edge Up: Alomar and Fomel: Non-stationary Previous: Triangle Smoothing Derivative
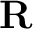 applied to data
applied to data
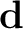 as
as
![$\mathbf{S}_R[\mathbf{d}]$](img30.png) and a triangle smoothing derivative operator as
and a triangle smoothing derivative operator as
![$\mathbf{S}_R'[\mathbf{d}]$](img31.png) .
Given the original data
.
Given the original data
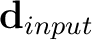 and the smoothed data
and the smoothed data
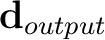 , we define the Taylor expansion
where
, we define the Taylor expansion
where
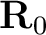 is the first guess for the radius and
is the first guess for the radius and
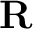 is the best estimate for the radius. Noting that
is the best estimate for the radius. Noting that
![$\mathbf{S}_R[\mathbf{d}_{input}] \approx \mathbf{d}_{output}$](img36.png) , we rearrange equation 13 to solve for
, we rearrange equation 13 to solve for 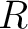 :
We can repeat this approach and solve for the radius iteratively, where the radius at the
:
We can repeat this approach and solve for the radius iteratively, where the radius at the 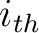 iteration is given by
The proposed method in theory converges with a rate approaching quadratic, although convergence is not guaranteed if the initial guess is far from the true value (Lawson and Hanson, 1995). The method is directly extended to solve for a non-stationary triangle smoothing radius given that both triangle smoothing and its derivative are non-stationary. Note that for stability of the solution, we must take care in performing the division in equation 15. We implement smooth division which treats division as inversion and regularizes the inversion in equation 15 using shaping regularization (Fomel, 2007b).
The shaping regularization is controlled by its own smoothness radius and reduces the radius estimation to stationary least-squares estimate when the smoothing radius for shaping is set to be very large.
iteration is given by
The proposed method in theory converges with a rate approaching quadratic, although convergence is not guaranteed if the initial guess is far from the true value (Lawson and Hanson, 1995). The method is directly extended to solve for a non-stationary triangle smoothing radius given that both triangle smoothing and its derivative are non-stationary. Note that for stability of the solution, we must take care in performing the division in equation 15. We implement smooth division which treats division as inversion and regularizes the inversion in equation 15 using shaping regularization (Fomel, 2007b).
The shaping regularization is controlled by its own smoothness radius and reduces the radius estimation to stationary least-squares estimate when the smoothing radius for shaping is set to be very large.