|
|
|
|
Well log interpolation guided by geologic distance |
Next: Numerical examples Up: Method Previous: Predictive painting
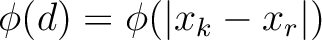 , whose value decays along the increasing distance (Micchelli, 1984).
An inverse quadratic form of the RBF is:
, whose value decays along the increasing distance (Micchelli, 1984).
An inverse quadratic form of the RBF is:
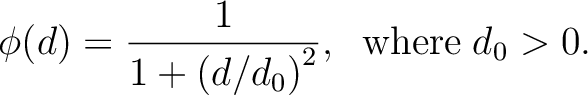 (2)
(2)
Then the interpolation can be calculated as below:
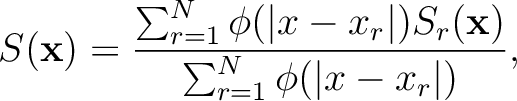 (3)
(3)
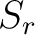 is the result of spreading well log at well location
is the result of spreading well log at well location 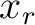 into the seismic data and
into the seismic data and 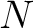 represents the total number of used wells.
represents the total number of used wells.
We propose to extend the definition of 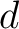 from simply the horizontal distance
from simply the horizontal distance
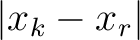 to the geologic distance that is measured along the seismic horizon:
to the geologic distance that is measured along the seismic horizon:
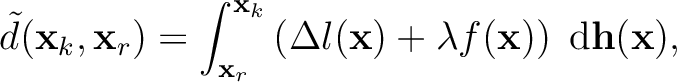 (4)
(4)
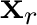 ,
, 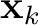 are points along a seismic horizon
are points along a seismic horizon
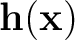 ;
;
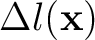 is the curve length of the horizon, it can be calculated by
is the curve length of the horizon, it can be calculated by
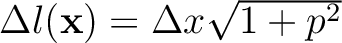 given local slope estimation
given local slope estimation 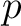 ;
; 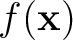 is fault attribute and
is fault attribute and 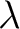 represents the distance penalty parameter, this term exaggerates the distance across fault.
The geologic distance indicates the decay of information confidence from the reference trace.
We perform this integration efficiently by accumulative predictive painting.
represents the distance penalty parameter, this term exaggerates the distance across fault.
The geologic distance indicates the decay of information confidence from the reference trace.
We perform this integration efficiently by accumulative predictive painting.