EMD-seislet transform

1D seislet transform

The seislet transform can be constructed by multi-scale prediction of the odd components 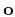$\mathbf{o}$ from the even components $\mathbf{e}$ :

$$\mathbf{r} =\mathbf{o}-\mathbf{P}(\mathbf{e}),$$ (2)

$$\mathbf{c} =\mathbf{e}+\mathbf{U}(\mathbf{r}).$$ (3)

In the above equations, 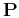$\mathbf{P}$ denotes the prediction operator and 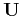$\mathbf{U}$ denotes the updating operator at a particular scale. 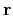$\mathbf{r}$ denotes the difference vector and $\mathbf{c}$ denotes the updated even component. The inverse seislet transform follows the inverse process of equations 2 and 3 continuing from large to small scale. The difference between the 1D seislet transform and the 1D wavelet transform is whether the prediction is modulated by an appropriate frequency. In the simplest case of Haar transform, the Z-transform domain prediction filter for the Haar wavelet transform is

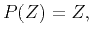$$P(Z)=Z,$$ (4)

and the Z-transform domain Haar prediction filter for wavelet transform is

$$U(Z)=Z/2.$$ (5)

However, for the seislet transform,

$$P(Z) =Z/Z_0,$$ (6)

$$U(Z) =1/2(Z/Z_0).$$ (7)

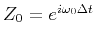where $Z_0=e^{i\omega_0\Delta t}$ . The prediction filter in equation 6 can perfectly characterize a sinusoid with 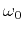$\omega_0$ angular frequency sampled on a 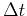$\Delta t$ grid. Analogously, the prediction filter for biorthogonal 2/2 transform can be expressed as:

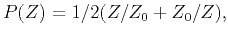$$P(Z)=1/2(Z/Z_0+Z_0/Z),$$ (8)

and its corresponding updating operator is

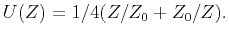$$U(Z)=1/4(Z/Z_0+Z_0/Z).$$ (9)

EMD-seislet transform