|
|
|
|
EMD-seislet transform |
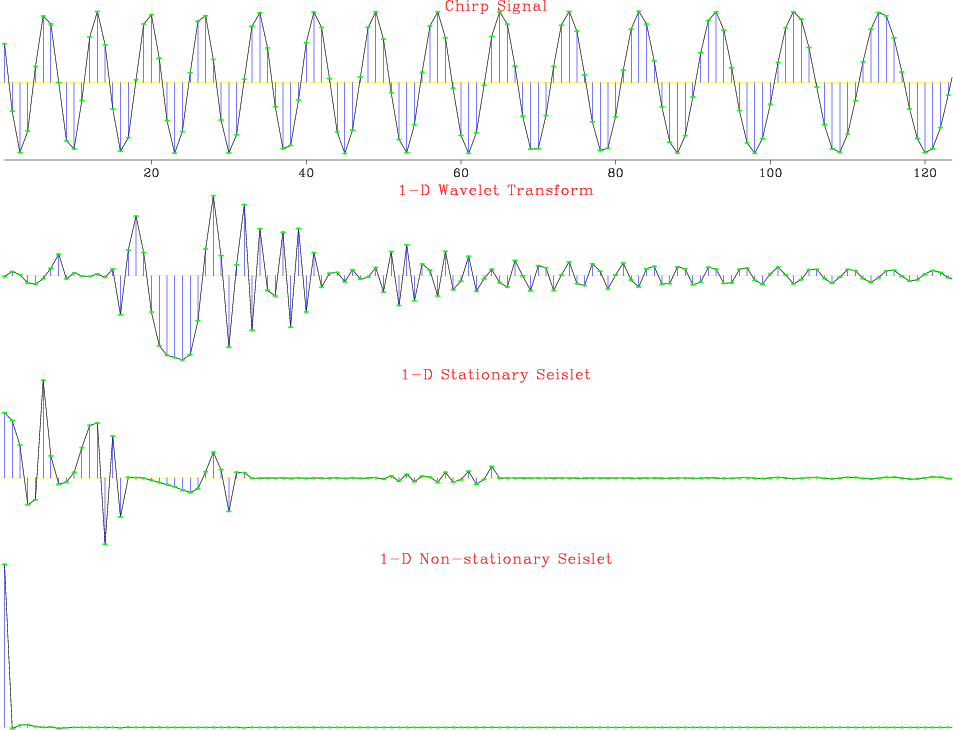
Figure 1 shows a comparison between the wavelet transform and the 1D stationary and non-stationary seislet transforms in compressing a 1D signal with smooth frequency components. The frequency ranges from 250 to 186 Hz. Both the wavelet transform and stationary seislet transform fail to compress the signal well while the non-stationary seislet transform obtains a perfectly sparse representation.
|
|---|
|
non-comp2
Figure 1. Demonstration of 1D non-stationary seislet transform for non-stationary signal. Upper: non-stationary chirp signal, frequency ranges from 250 to 186 Hz. Upper middle: compressed using 1D wavelet transform. Down middle: compressed using 1D stationary seislet transform with the frequency of 250 Hz. Down: compressed using 1D non-stationary seislet transform. |
|
|
|
|
|
|
EMD-seislet transform |