Next: 1D seislet transform
Up: Method
Previous: Method
The process of EMD has the following simple expression:
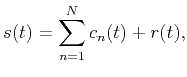 |
(1) |
where 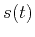 is the original non-stationary signal,
is the original non-stationary signal, 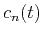 (
(
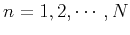 ) denotes each separated IMF,
) denotes each separated IMF,  denotes the number of separated IMF, and
denotes the number of separated IMF, and 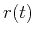 denotes the residual after EMD. The process of EMD is to gradually remove the stable oscillations embedded in the original signal to arrive at a monotonic and smooth residual or trend at last. A special property of the EMD is that the IMFs represent different oscillations embedded in the data, where the oscillating frequency for each sub-signal
denotes the residual after EMD. The process of EMD is to gradually remove the stable oscillations embedded in the original signal to arrive at a monotonic and smooth residual or trend at last. A special property of the EMD is that the IMFs represent different oscillations embedded in the data, where the oscillating frequency for each sub-signal 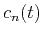 decreases with IMF order increasing (Huang et al., 1998).
decreases with IMF order increasing (Huang et al., 1998).
2019-02-12