 |
 |
 |
 | Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |  |
![[pdf]](icons/pdf.png) |
Next: Homogeneous Media
Up: Theory
Previous: Theory
Following the notation of Du et al. (2014), a generic linear second-order in time wave equation can be expressed in the following form
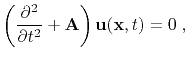 |
(1) |
where
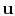 is the wavefield,
is the wavefield,
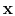 is the spatial location,
is the spatial location,  is time, and
is time, and
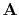 is the a matrix operator containing material parameters and spatial derivative operators. Equation 1 can also be expressed using the first-order system
is the a matrix operator containing material parameters and spatial derivative operators. Equation 1 can also be expressed using the first-order system
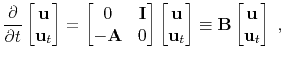 |
(2) |
where
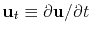 . The solution of equation 2 can be formulated using the definition of the matrix exponential:
. The solution of equation 2 can be formulated using the definition of the matrix exponential:
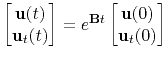 |
(3) |
Defining
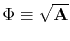 , the eigenvalue decomposition of
, the eigenvalue decomposition of
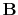 can be written as (Du et al., 2014)
can be written as (Du et al., 2014)
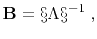 |
(4) |
where
The solution to the first-order system 3 can now be written as
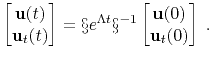 |
(6) |
To simplify the system, we can define the analytical wavefield
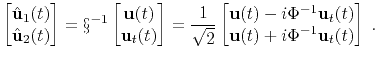 |
(7) |
The solution to equation 1 finally takes the form
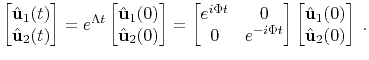 |
(8) |
Selecting the first of the two decoupled solutions of equation 8 leads to a time extrapolation operator
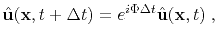 |
(9) |
where
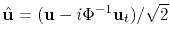 .
.
For acoustic isotropic constant-density wave equations for pressure waves,
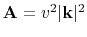 where
where 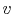 is velocity and
is velocity and
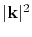 is the Laplacian operator. This corresponds to the one-step extrapolation method proposed by (Zhang and Zhang, 2009).
is the Laplacian operator. This corresponds to the one-step extrapolation method proposed by (Zhang and Zhang, 2009).
The wavefield
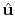 is an analytical signal, with its imaginary part being the Hilbert transform of its real part (Zhang and Zhang, 2009). To see this, we can perform Hilbert transform to the real-valued wavefield
is an analytical signal, with its imaginary part being the Hilbert transform of its real part (Zhang and Zhang, 2009). To see this, we can perform Hilbert transform to the real-valued wavefield
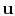 in the frequency domain, and use the dispersion relation
in the frequency domain, and use the dispersion relation
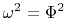 and derivative property of Fourier Transform
and derivative property of Fourier Transform
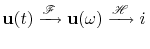 sign sign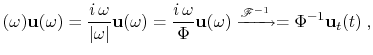 |
(10) |
where
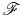 and
and
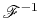 denotes forward and inverse Fourier transform in time. The output corresponds to the imaginary part of analytical wavefield
denotes forward and inverse Fourier transform in time. The output corresponds to the imaginary part of analytical wavefield
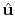 .
.
 |
 |
 |
 | Recursive integral time extrapolation of elastic waves using low-rank symbol approximation |  |
![[pdf]](icons/pdf.png) |
Next: Homogeneous Media
Up: Theory
Previous: Theory
2018-11-16
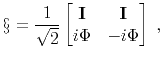
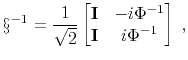
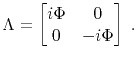
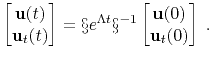
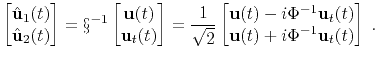
![]() where
where ![]() is velocity and
is velocity and
![]() is the Laplacian operator. This corresponds to the one-step extrapolation method proposed by (Zhang and Zhang, 2009).
is the Laplacian operator. This corresponds to the one-step extrapolation method proposed by (Zhang and Zhang, 2009).
![]() is an analytical signal, with its imaginary part being the Hilbert transform of its real part (Zhang and Zhang, 2009). To see this, we can perform Hilbert transform to the real-valued wavefield
is an analytical signal, with its imaginary part being the Hilbert transform of its real part (Zhang and Zhang, 2009). To see this, we can perform Hilbert transform to the real-valued wavefield
![]() in the frequency domain, and use the dispersion relation
in the frequency domain, and use the dispersion relation
![]() and derivative property of Fourier Transform
and derivative property of Fourier Transform