Double sparsity dictionary for seismic noise attenuation

Seislet transform based DSD

The analysis model can be used only if the base transform is invertible and can be more convenient to straightforwardly cascade two types of transforms: the base transform and the learning-based dictionary. In this paper, we use the seislet transform (Fomel and Liu, 2010) as the base transform and DDTF (Cai et al., 2013) as the learning-based dictionary to construct the proposed DSD framework, following the aforementioned algorithm. The DDTF refers exactly to the process of solving equations 7 and 8. In the seislet based DSD, the seislet dictionary $\mathbf{B}$ is substituted by the combined dictionary $\mathbf{BW}$ . The effective atoms we obtain are thus interpolated version of the atoms in the learning-based dictionary DDTF, interpolated by the seislet transform process. The seislet based DSD thus enjoys the structure-oriented multi-scale capabilities of the seislet transform while adding information to it specific to the training domain. It should also be mentioned that because of the initial seislet decomposition, each sub-band in the transform domain can be treated separately and thus can has its own sub-dictionary (Ophir et al., 2011).

We train the filters patch by patch of the whole dataset. We apply the maximally overlapping patches (i.e., the two neighbor patches only shifted by one column) for the training. This creates a richness in the training data and leads to a shift-invariance for the dictionary. In the DDTF, for each patch, the training filer is orthogonal, but the full transform matrix $\mathbf{W}$ (each column is a training filter on patches) is redundant. Because of the base seislet transform, the DDTF trains the dictionary from a multi-scale seislet domain instead of the single scale domain of the original data. Although we follow the same strategy as Ophir et al. (2011), we utilize different tools for the two main components in the multi-scale learning framework. The DDTF used in the proposed method is much faster than the K-SVD method used by Ophir et al. (2011), and the seislet transform used in the proposed method is more appropriate for seismic data than the wavelets used by Ophir et al. (2011). In K-SVD, there exists a large number of patches for training and the components of the dictionary are updating individually (indicating many SVD decompositions). However, the DDTF method updates all the components (columns of $\mathbf{W}$ ) by one SVD decomposition (Yu et al., 2015), thus is more efficient. Besides, because of the learning efficiency in DDTF, the DDTF based approaches can be applicable to high-dimensional denoising and interpolation problems. The seislet transform, however, is superior than traditional wavelet transform for compressing seismic data because it utilizes local slope to construct the transform. The superior performance of seislet transform over state-of-the-art transforms in denoising, interpolation, and deblending of seismic data have been demonstrated in a number of references (Gan et al., 2015; Chen et al., 2014; Fomel and Liu, 2010; Liu and Fomel, 2010). Thus, the combination between the seislet transform and DDTF through the DSD framework seems very appealing.

The cascaded DSD framework, combined with thresholding-based denoising, can be briefly summarized as follows:

1. Apply the seislet transform to noisy seismic data.
2. Apply the DDTF to each band in the seislet domain to form DSD domain.
3. Perform thresholding in the DSD domain.
4. Apply the adjoint DDTF to the thresholded data in DSD domain.
5. Apply the inverse seislet transform to recover the denoised data.

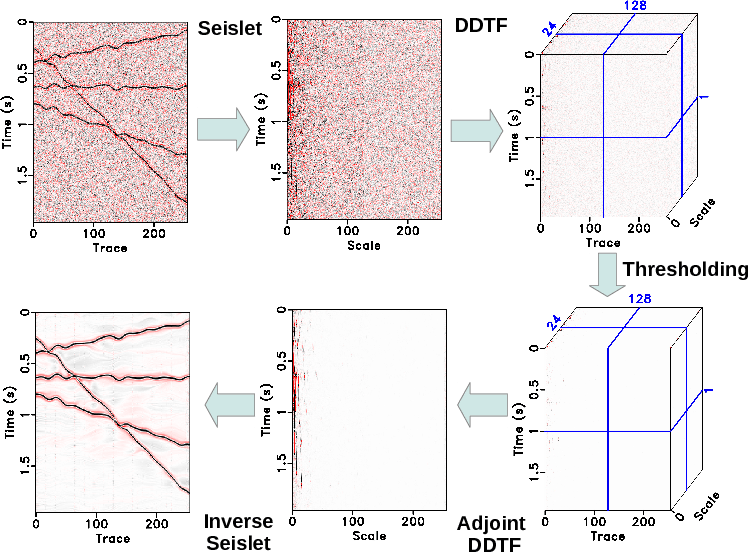
There is an inner iterative process in the above steps when applying the DDTF. It refers to applying the DDTF by the data-driven learning process following equations 6 to 8. The iterative process acts as a training step for the DDTF, and the trained dictionary $\mathbf{W}$ are finally used to transform the seislet subband data into the double-sparsity domain and used for the adjoint DDTF step in step 4. Figure 1 shows a demonstration of denoising processes of the proposed DSD. It also shows the seislet transform domain and DSD transform domain before and after thresholding.

demo2
Figure 1. Demonstration of the DSD-based denoising processes.

Double sparsity dictionary for seismic noise attenuation