The transformation of the 4D data hypercube at a single frequency into a level-four block Hankel matrix can be represented in operator notation as follows:
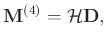 |
(5) |
where
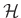 denotes the Hankelization operator. To avoid notational clutter, we omit the argument
denotes the Hankelization operator. To avoid notational clutter, we omit the argument
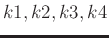 of
of
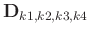 for convenience. In general, the level-four block Hankel matrix
for convenience. In general, the level-four block Hankel matrix
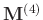 can be represented as:
can be represented as:
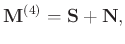 |
(6) |
where
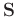 and
and
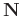 denote the level-four block Hankel matrices of signal and random noise, respectively. Here, missing signal can be regarded as a condition where signal and noise are summed to zero, and is distributed randomly due to the irregular sampling. Therefore, missing data represents itself by the noise-like characteristics.
denote the level-four block Hankel matrices of signal and random noise, respectively. Here, missing signal can be regarded as a condition where signal and noise are summed to zero, and is distributed randomly due to the irregular sampling. Therefore, missing data represents itself by the noise-like characteristics.
We assume that
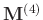 and
and
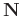 have full rank. The size of
have full rank. The size of
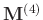 is
is
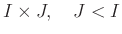 .
.
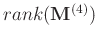 =
=
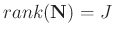 ,
,
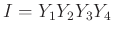 ,
,
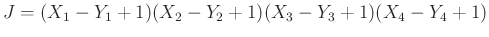 , and
, and
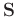 has deficient rank,
has deficient rank,
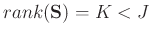 . The singular value decomposition (SVD) of
. The singular value decomposition (SVD) of
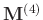 can be represented as:
can be represented as:
![$\displaystyle \mathbf{M}^{(4)} = [\mathbf{U}_1^{M^{(4)}}\quad \mathbf{U}_2^{M^{...
...c}
(\mathbf{V}_1^{M^{(4)}})^H\\
(\mathbf{V}_2^{M^{(4)}})^H
\end{array}\right],$](img54.png) |
(7) |
where
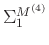 (
(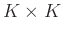 ) and
) and
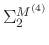 (
(
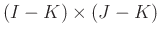 ) are diagonal matrices and contain, respectively, larger singular values and smaller singular values.
) are diagonal matrices and contain, respectively, larger singular values and smaller singular values.
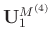 (
(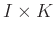 ),
),
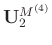 (
(
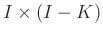 ),
),
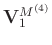 (
(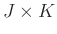 ) and
) and
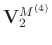 (
(
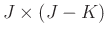 ) denote the associated matrices with singular vectors. The symbol
) denote the associated matrices with singular vectors. The symbol ![$[\cdot]^H$](img67.png) denotes the conjugate transpose of a matrix. Generally, the signal is more energy-concentrated and correlative than the random noise. Thus, the larger singular values and their associated singular vectors represent the signal, while the smaller values and their associated singular vectors represent the random noise. We substitute
denotes the conjugate transpose of a matrix. Generally, the signal is more energy-concentrated and correlative than the random noise. Thus, the larger singular values and their associated singular vectors represent the signal, while the smaller values and their associated singular vectors represent the random noise. We substitute
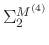 with
with
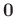 to achieve the goal of attenuating random noise while recovering the missing data during the first iteration in reconstruction process as follows:
to achieve the goal of attenuating random noise while recovering the missing data during the first iteration in reconstruction process as follows:
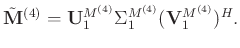 |
(8) |
Equation 8 is referred to as the TSVD, which is used in the conventional rank-reduction approach for 5D seismic data interpolation.
Nevertheless,
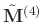 is actually still contaminated with residual random noise. Following Huang et al. (2016), here we briefly clarify the reason why the
is actually still contaminated with residual random noise. Following Huang et al. (2016), here we briefly clarify the reason why the
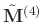 is still corrupted with some residual random noise. We first consider the SVD of the signal component
is still corrupted with some residual random noise. We first consider the SVD of the signal component
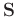 in a way similar to equation 7:
in a way similar to equation 7:
![$\displaystyle \mathbf{S} = [\mathbf{U}_1^{S}\quad \mathbf{U}_2^{S}]\left[\begin...
...egin{array}{c}
(\mathbf{V}_1^{S})^H\\
(\mathbf{V}_2^{S})^H
\end{array}\right].$](img71.png) |
(9) |
Different from
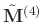 , the signal matrix should be of deficient rank, then
, the signal matrix should be of deficient rank, then
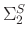 is a zero diagonal matrix, and
is a zero diagonal matrix, and
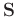 can be denoted in a concise form:
can be denoted in a concise form:
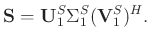 |
(10) |
Combining equations 6, 9, and 10, it straightforwardly derive the following equation:
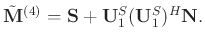 |
(11) |
The appendix A gives a detailed derivation for obtaining equation 11, which we call exact formulation of the block Hankel matrix. From equation 11, we can intuitively know that TSVD result
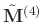 still contains significant random noise
still contains significant random noise
 , or in other words, the traditional TSVD can only decompose the data space into a mixture of signal and noise subspace.
, or in other words, the traditional TSVD can only decompose the data space into a mixture of signal and noise subspace.
2020-12-05
![]() and
and
![]() have full rank. The size of
have full rank. The size of
![]() is
is
![]() .
.
![]() =
=
![]() ,
,
![]() ,
,
![]() , and
, and
![]() has deficient rank,
has deficient rank,
![]() . The singular value decomposition (SVD) of
. The singular value decomposition (SVD) of
![]() can be represented as:
can be represented as:
![]() is actually still contaminated with residual random noise. Following Huang et al. (2016), here we briefly clarify the reason why the
is actually still contaminated with residual random noise. Following Huang et al. (2016), here we briefly clarify the reason why the
![]() is still corrupted with some residual random noise. We first consider the SVD of the signal component
is still corrupted with some residual random noise. We first consider the SVD of the signal component
![]() in a way similar to equation 7:
in a way similar to equation 7: