Consider a block of 5D data
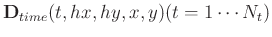 , where
, where 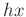 ,
, 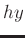 ,
, 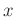 ,
, 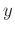 denote
denote 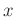 and
and 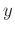 offsets and
offsets and 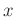 and
and 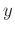 midpoints. The rank-reduction method operates on the 5D seismic data in the following way: first, rank-reduction method transforms
midpoints. The rank-reduction method operates on the 5D seismic data in the following way: first, rank-reduction method transforms
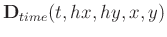 into
into
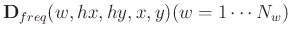 of complex values in the frequency domain. In the condition that the spatial variables are regularly sampled, each observation at a given frequency slice can be represented via a 4D spatial hypercube
of complex values in the frequency domain. In the condition that the spatial variables are regularly sampled, each observation at a given frequency slice can be represented via a 4D spatial hypercube
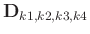 with
with
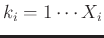 ,
, 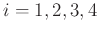 . In order to make our target matrices close to square matrices, parameters
. In order to make our target matrices close to square matrices, parameters 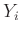 are defined as
are defined as
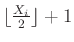 ,
, 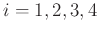 . Gao et al. (2015a) outlined the usefulness of square Hankel matrices in rank reduction based regularization and described why square matrices are preferred. The symbol
. Gao et al. (2015a) outlined the usefulness of square Hankel matrices in rank reduction based regularization and described why square matrices are preferred. The symbol
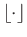 denotes the integer part of its argument. The 4D spatial hypercube
denotes the integer part of its argument. The 4D spatial hypercube
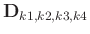 can be embedded in a level-four block Hankel matrix as follows. We have to address in advance that each frequency slice of data is operated the exactly same way. We first embed the seismic data in a level-one Hankel matrix using all data components in the first dimension of the tensor
can be embedded in a level-four block Hankel matrix as follows. We have to address in advance that each frequency slice of data is operated the exactly same way. We first embed the seismic data in a level-one Hankel matrix using all data components in the first dimension of the tensor
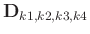 at a given frequency
at a given frequency 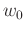 . This generates the following Hankel matrices,
. This generates the following Hankel matrices,
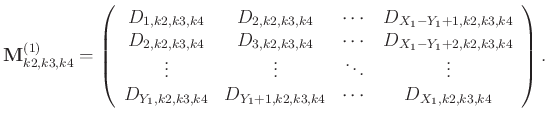 |
(1) |
Matrices in Equation 1 are of size
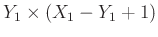 . These matrices are embedded in a level-two block Hankel matrix:
. These matrices are embedded in a level-two block Hankel matrix:
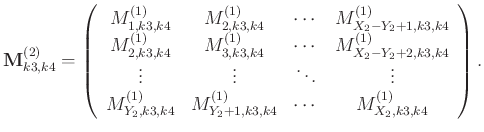 |
(2) |
Matrices in Equation 2 are of size
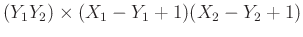 . These matrices are now embedded in a level-three block Hankel matrix:
. These matrices are now embedded in a level-three block Hankel matrix:
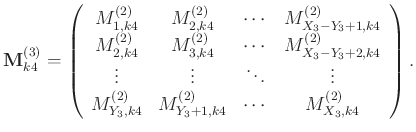 |
(3) |
Matrices in Equation 3 are of size
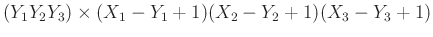 . At last, these matrices are embedded in our final target level-four block Hankel matrix:
. At last, these matrices are embedded in our final target level-four block Hankel matrix:
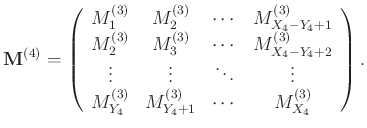 |
(4) |
Equation 4 is the target matrix of our problem. The size of level-four block Hankel matrix
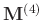 is
is
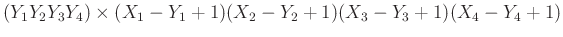 . If
. If 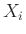 is an odd integer, the size of
is an odd integer, the size of
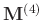 is
is
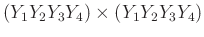 .
.
2020-12-05
![]() . These matrices are embedded in a level-two block Hankel matrix:
. These matrices are embedded in a level-two block Hankel matrix:
![]() . These matrices are now embedded in a level-three block Hankel matrix:
. These matrices are now embedded in a level-three block Hankel matrix:
![]() . At last, these matrices are embedded in our final target level-four block Hankel matrix:
. At last, these matrices are embedded in our final target level-four block Hankel matrix:
![]() is
is
![]() . If
. If ![]() is an odd integer, the size of
is an odd integer, the size of
![]() is
is
![]() .
.