|
|
|
|
Effects of lateral heterogeneity on time-domain processing parameters |
Next: Appendix B Derivation of Up: Appendix A Review of Previous: Reflection traveltime
As a more fundamental alternative to study seismic responses, one can choose to consider a reflecting point (scatterer) instead of a reflecting surface because any model is a superposition of such scatterers. Assuming that the subsurface velocity 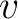 is constant, the total (diffraction) traveltime of the wave traveling in this configuration is simply a sum of traveltime of the two legs, which can be expressed by the double-square-root (DSR) equation (Claerbout, 1996):
is constant, the total (diffraction) traveltime of the wave traveling in this configuration is simply a sum of traveltime of the two legs, which can be expressed by the double-square-root (DSR) equation (Claerbout, 1996):
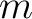 denotes midpoint,
denotes midpoint, 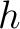 denotes half offset,
denotes half offset, 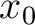 denotes the horizontal coordinate of the point scatterer, and
denotes the horizontal coordinate of the point scatterer, and 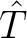 is a one-way vertical traveltime from the point scatterer to the surface. The true location of the point scatterer
is a one-way vertical traveltime from the point scatterer to the surface. The true location of the point scatterer 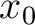 will also be the same as the emerging location of the image rays (Hubral, 1977).
will also be the same as the emerging location of the image rays (Hubral, 1977).
In the more general case of varying subsurface velocity, equation (32) becomes an approximation for diffraction traveltime that is routinely used in prestack time migration (Yilmaz, 2001). 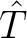 then denotes the one-way traveltime of the image ray from the point scatter to the surface and the escape location
then denotes the one-way traveltime of the image ray from the point scatter to the surface and the escape location 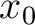 of the image ray will generally be different from the true location of the point scatterer in the Cartesian coordinates. The velocity
of the image ray will generally be different from the true location of the point scatterer in the Cartesian coordinates. The velocity 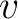 becomes time-migration velocity
becomes time-migration velocity 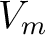 , which will be selected for the best fit traveltime to equation (32).
, which will be selected for the best fit traveltime to equation (32).
To further understand equation (32) in heterogeneous media, we follow the derivation by () and consider the general one-way traveltime approximation centered around the image ray from the point scatterer to any surface point 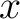 given by,
given by,
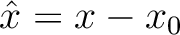 denotes the distance between the escape location
denotes the distance between the escape location 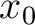 and any surrounding point
and any surrounding point 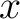 on the surface. Note that
on the surface. Note that 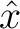 functions similarly to
functions similarly to 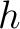 in equation (5) but has a different meaning than the conventional half offset when considering reflection traveltime. The first-order term in equation (33) is always equal to zero due to the image rays always having zero phase slowness tangent to the surface, or equivalently to
in equation (5) but has a different meaning than the conventional half offset when considering reflection traveltime. The first-order term in equation (33) is always equal to zero due to the image rays always having zero phase slowness tangent to the surface, or equivalently to
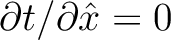 at
at 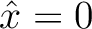 . We emphasize the notable presence of possible third-order term (
. We emphasize the notable presence of possible third-order term (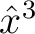 ). This term can be neglected when
). This term can be neglected when 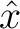 is sufficiently small or when the medium under consideration provides additional symmetry to the function of traveltime such as in homogeneous or horizontally layered VTI media, where traveltime varies as an even function around
is sufficiently small or when the medium under consideration provides additional symmetry to the function of traveltime such as in homogeneous or horizontally layered VTI media, where traveltime varies as an even function around 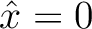 . Converting equation (33) to a series in traveltime squared gives
Using equation (34), we can compute the total traveltime from a source at
. Converting equation (33) to a series in traveltime squared gives
Using equation (34), we can compute the total traveltime from a source at 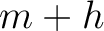 to point scatterer and to a receiver at
to point scatterer and to a receiver at 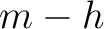 as follows,
Equation (35) suggests that equation (32) simply represents a sum of two Taylor expansions of the one-way traveltime from the point scatterer to the source and the receiver. Therefore, the migration velocity
as follows,
Equation (35) suggests that equation (32) simply represents a sum of two Taylor expansions of the one-way traveltime from the point scatterer to the source and the receiver. Therefore, the migration velocity 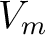 can be related to the one-way traveltime derivatives as shown in equation (7). Moreover, our proposed framework to study the effects of weak lateral heterogeneity on one-way traveltime is applicable to
can be related to the one-way traveltime derivatives as shown in equation (7). Moreover, our proposed framework to study the effects of weak lateral heterogeneity on one-way traveltime is applicable to 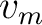 provided that the image ray is assumed to be sufficiently close to the vertical direction, which is exactly true in the case of 1D layered anisotropic media with horizontal symmetry planes.
provided that the image ray is assumed to be sufficiently close to the vertical direction, which is exactly true in the case of 1D layered anisotropic media with horizontal symmetry planes.