 |
 |
 |
 | A variational formulation
of the fast marching eikonal solver |  |
![[pdf]](icons/pdf.png) |
Next: Conforming Triangulation
Up: Fomel: Fast marching
Previous: Acknowledgments
-
Abgrall, R., 1996, Numerical discretization of the first-order
Hamilton-Jacobi equation on triangular meshes: Comm. on Pure and Applied
Math., XLIX, 1339-1373.
-
-
Abgrall, R., and J. D. Benamou, 1996, Multivalued traveltime fields, ray
tracing and eikonal solver on unstructured grids: 66th Ann. Internat. Mtg,
Soc. of Expl. Geophys., 1208-1211.
-
-
Albertin, U. K., and W. Wiggins, 1994, Embedding geologic horizon surfaces in
tetrahedral meshes for geologic modeling: 64th Ann. Internat. Mtg, Soc. of
Expl. Geophys., 502-505.
-
-
Alkhalifah, T., and S. Fomel, 1997, Implementing the fast marching eikonal
solver: Spherical versus cartesian coordinates, in SEP-95: Stanford
Exploration Project, 149-171.
-
-
Biondi, B., S. Fomel, and T. Alkhalifah, 1997, ``Focusing'' eikonal equation
and global tomography, in SEP-95: Stanford Exploration Project,
61-76.
-
-
Cao, S., and S. A. Greenhalgh, 1994, Finite-difference solution of the eikonal
equation using an efficient, first-arrival wavefront tracking scheme:
Geophysics, 59, 632-643.
- (Errata in GEO-64-03-992).
-
Chew, L. P., 1989, Constrained Delaunay triangulations: Algorithmica, 4, 97-108.
-
-
Cormen, T. H., C. E. Leiserson, and R. L. Rivest, 1990, Introduction to
algorithms: McGraw-Hill.
-
-
Delaunay, B. N., 1934, Sur la sphère vide: Izv. Akad. Nauk SSSR, Otdel.
Mat. Est. Nauk, 7, 793-800.
-
-
Dellinger, J., 1991, Anisotropic finite-difference traveltimes: 61st Ann.
Internat. Mtg, Soc. of Expl. Geophys., 1530-1533.
-
-
Dijkstra, E. W., 1959, A note on two problems in connection with graphs:
Numer. Math., 1, 269-271.
-
-
Edelsbrunner, H., and T. S. Tan, 1993, An upper bound for conforming
Delaunay triangulation: Discrete Comput. Geom., 10, 197-213.
-
-
Fomel, S., 1995, Amplitude preserving offset continuation in theory Part 1:
The offset continuation equation, in SEP-84: Stanford Exploration
Project, 179-198.
-
-
----, 1996, Migration and velocity analysis by velocity continuation, in SEP-92: Stanford Exploration Project, 159-188.
-
-
Fortune, S., 1987, A sweepline algorithm for Voronoi diagram: Algorithmica,
2, 153-174.
-
-
Garland, M., and P. S. Heckbert, 1996, Fast and flexible polygonization of
height fields, in Visual Proceedings: SIGGRAPH 96, 143.
-
-
Guibas, L., and J. Stolfi, 1985, Primitives for the manipulation of general
subdivisions and the computation of Voronoi diagrams: ACM Trans. Graphics,
4, 74-123.
-
-
Guibas, L. J., D. Knuth, and M. Sharir, 1992, Randomized incremental
construction of Delaunay and Voronoi diagrams: Algorithmica, 7,
381-413.
-
-
Guiziou, J. L., J. L. Mallet, P. Nobili, R. Anandappane, and P. Thisse, 1991,
3-D ray-tracing through complex triangulated surfaces: 61st Ann. Internat.
Mtg, Soc. of Expl. Geophys., 1497-1500.
-
-
Hale, D., and J. K. Cohen, 1991, Triangulated models of the Earth's
subsurface: Center for Wave Phenomenon Report, CWP-107.
-
-
Hansen, A. J., and P. L. Levin, 1992, On conforming Delaunay mesh
generation: Adv. in Eng. Soft., 14, 129-135.
-
-
Lanczos, C., 1966, The variational principles of mechanics: University of
Toronto Press.
-
-
Lee, D. T., and A. K. Lin, 1986, Generalized Delaunay triangulation for
planar graphs: Discrete Comput. Geom., 1, 201-217.
-
-
Lions, P. L., 1982, Generalized solutions of Hamilton-Jacobi equations:
Pitman.
-
-
Moser, T. J., 1991, Shortest path calculation of seismic rays: Geophysics,
56, 59-67.
-
-
Osher, S., and J. A. Sethian, 1988, Fronts propagating with
curvature-dependent speed: Algorithms based on Hamilton-Jacobi
formulation: Jour. of Comp. Phys., 79, 12-49.
-
-
Podvin, P., and I. Lecomte, 1991, Finite difference computation of traveltimes
in very contrasted velocity models: A massively parallel approach and its
associated tools: Geophysical Journal International, 105, 271-284.
-
-
Qin, F., Y. Luo, K. B. Olsen, W. Cai, and G. T. Schuster, 1992,
Finite-difference solution of the eikonal equation along expanding
wavefronts: Geophysics, 57, 478-487.
-
-
Rivara, M.-C., 1996, New mathematical tools and techniques for the refinement
and/or improvement of unstructured triangulations, in Proceedings: 5th
International Meshing Roundtable, 77-86.
-
-
Ruppert, J., 1995, A Delaunay refinement algorithm for quality
two-dimensional mesh generation: Journal of Algorithms, 18, 548-585.
-
-
Sethian, J. A., 1996a, A fast marching level set method for monotonically
advancing fronts: Proc. Nat. Acad. Sci., 93, 1591-1595.
-
-
----, 1996b, Level set methods: Evolving interfaces in geometry, fluid
mechanics, computer vision, and materials science: Cambridge University
Press.
-
-
Sethian, J. A., and A. M. Popovici, 1997, Three-dimensional traveltime
computation using the fast marching method: submitted to Geophysics.
-
-
Shamos, M., and D. Hoey, 1975, Closest point problems, in Proceedings:
16th Annual IEEE Sympos. Found. Comput. Sci., 151-162.
-
-
Shewchuk, J. R., 1996, Robust adaptive floating-point geometric predicates,
in 12th Annual Symposium on Computational Geometry: Association for
Computing Machinery, 141-150.
-
-
Sibson, R., 1978, Locally equiangular triangulations: Comput. J., 21,
243-245.
-
-
Smirnov, V. I., 1964, A course on higher mathematics: Pergamon Press.
-
-
Stankovic, G. M., and U. K. Albertin, 1995, Raytracing in topological
tetrahedral models: 65th Ann. Internat. Mtg, Soc. of Expl. Geophys.,
1247-1250.
-
-
van Trier, J., and W. W. Symes, 1991, Upwind finite-difference calculation of
traveltimes: Geophysics, 56, 812-821.
-
-
Vidale, J. E., 1990, Finite-difference calculation of traveltimes in three
dimensions: Geophysics, 55, 521-526.
-
-
Wiggins, W., U. K. Albertin, and G. Stankovic, 1993, Building 3-D depth
migration velocity models with topological objects: 63rd Ann. Internat. Mtg,
Soc. of Expl. Geophys., 170-173.
-
-
Woo, M., J. Neider, and T. Davis, 1997, OpenGL programming guide:
Addison-Wesley.
-
Appendix
A
Incremental DELAUNAY TRIANGULATION and related problems
Delaunay triangulation (Guibas and Stolfi, 1985; Delaunay, 1934; Sibson, 1978) is a fundamental
geometric construction, which has numerous applications in different
computational problems. For a given set of nodes (points on the
plane), Delaunay triangulation constructs a triangle tessellation of
the plane with the initial nodes as vertices. Among all possible
triangulations, the Delaunay triangulation possesses optimal
properties, which make it very attractive for practical applications,
such as computational mesh generation. One of the most well-known
properties is maximizing the minimum triangulation angle. In three
dimensions, Delaunay triangulation generalizes naturally to a
tetrahedron tessellation.
Several optimal-time algorithms of Delaunay triangulation (and its
counterpart-Voronoi diagram) have been proposed in the literature.
The divide-and-conquer algorithm (Guibas and Stolfi, 1985; Shamos and Hoey, 1975) and the
sweep-line algorithm (Fortune, 1987) both achieve the optimal  worst-case time complexity. Alternatively, a family of
incremental algorithms has been used in practice because of their
simplicity and robustness. Though the incremental algorithm can take
worst-case time complexity. Alternatively, a family of
incremental algorithms has been used in practice because of their
simplicity and robustness. Though the incremental algorithm can take
 time in the worst case, the expectation time can still be
time in the worst case, the expectation time can still be  , provided that the nodes are inserted in a random order
(Guibas et al., 1992).
, provided that the nodes are inserted in a random order
(Guibas et al., 1992).
The incremental algorithm consists of two main parts:
- Locate a triangle (or an edge), containing the inserted point.
- Insert the point into the current triangulation, making the
necessary adjustments.
The Delaunay criterion can be reduced in the second step to a simple
InCircle test (Guibas and Stolfi, 1985): if a circumcircle of a triangle
contains another triangulation vertex in its circumcenter, then the
edge between those two triangles should be ``flipped'' so that two new
triangles are produced. The testing is done in a recursive fashion
consistent with the incremental nature of the algorithm. When a new
node is inserted inside a triangle, three new triangles are created,
and three edges need to be tested. When the node falls on an edge,
four triangles are created, and four edges are tested. In the case of
test failure, a pair of triangles is replaced by the flip operation
with another pair, producing two more edges to test. Under the
randomization assumption, the expected total time of point insertion
is  . Randomization can be considered as an external part of
the algorithm, provided by preprocessing.
. Randomization can be considered as an external part of
the algorithm, provided by preprocessing.
Guibas et al. (1992) reduce the point location step to an efficient  procedure by maintaining a hierarchical tree structure: all
triangles, occurring in the incremental triangulation process, are
kept in memory, associated with their ``parents.'' One or two point
location tests (CCW tests) are sufficient to move to a lower
level of the tree. The search terminates with a current Delaunay
triangle.
procedure by maintaining a hierarchical tree structure: all
triangles, occurring in the incremental triangulation process, are
kept in memory, associated with their ``parents.'' One or two point
location tests (CCW tests) are sufficient to move to a lower
level of the tree. The search terminates with a current Delaunay
triangle.
To test the algorithmic performance of the incremental construction, I
have profiled the execution time of my incremental triangulation
program with the Unix pixie utility. The profiling result,
shown in Figures H-1 and H-2, complies
remarkably with the theory:  operations for the point
location step, and
operations for the point
location step, and  operations for the point insertion step.
The experimental constant for the insertion step time is about
operations for the point insertion step.
The experimental constant for the insertion step time is about  .
The experimental constant for the point location step is
.
The experimental constant for the point location step is  . The CPU
time, depicted in Figure H-3, also shows the expected
. The CPU
time, depicted in Figure H-3, also shows the expected  behavior.
behavior.
itime
Figure A-1. The number of point insertion operations
(InCircle test) plotted against the number of points.
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
ctime
Figure A-2. Number of point location operations
(CCW test) plotted against the number of points.
|
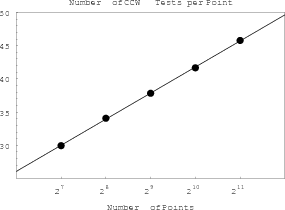
|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
time
Figure A-3. CPU time (in seconds per point) plotted
against the number of points.
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
A straightforward implementation of Delaunay triangulation would
provide an optimal triangulation for any given set of nodes. However,
the quality of the result for unfortunate geometrical
distributions of the nodes can be unsatisfactory. In the rest of this
appendix, I describe three problems, aimed at improving the
triangulation quality: conforming triangulation, triangulation of
height fields, and mesh refinement. Each of these problems can be
solved with a variation of the incremental algorithm.
Subsections
 |
 |
 |
 | A variational formulation
of the fast marching eikonal solver |  |
![[pdf]](icons/pdf.png) |
Next: Conforming Triangulation
Up: Fomel: Fast marching
Previous: Acknowledgments
2013-03-03
![]() worst-case time complexity. Alternatively, a family of
incremental algorithms has been used in practice because of their
simplicity and robustness. Though the incremental algorithm can take
worst-case time complexity. Alternatively, a family of
incremental algorithms has been used in practice because of their
simplicity and robustness. Though the incremental algorithm can take
![]() time in the worst case, the expectation time can still be
time in the worst case, the expectation time can still be ![]() , provided that the nodes are inserted in a random order
(Guibas et al., 1992).
, provided that the nodes are inserted in a random order
(Guibas et al., 1992).
![]() . Randomization can be considered as an external part of
the algorithm, provided by preprocessing.
. Randomization can be considered as an external part of
the algorithm, provided by preprocessing.
![]() procedure by maintaining a hierarchical tree structure: all
triangles, occurring in the incremental triangulation process, are
kept in memory, associated with their ``parents.'' One or two point
location tests (CCW tests) are sufficient to move to a lower
level of the tree. The search terminates with a current Delaunay
triangle.
procedure by maintaining a hierarchical tree structure: all
triangles, occurring in the incremental triangulation process, are
kept in memory, associated with their ``parents.'' One or two point
location tests (CCW tests) are sufficient to move to a lower
level of the tree. The search terminates with a current Delaunay
triangle.
![]() operations for the point
location step, and
operations for the point
location step, and ![]() operations for the point insertion step.
The experimental constant for the insertion step time is about
operations for the point insertion step.
The experimental constant for the insertion step time is about ![]() .
The experimental constant for the point location step is
.
The experimental constant for the point location step is ![]() . The CPU
time, depicted in Figure H-3, also shows the expected
. The CPU
time, depicted in Figure H-3, also shows the expected ![]() behavior.
behavior.


