|
|
|
|
Iterative least-square inversion for amplitude balancing |
In a seismic survey, the amplitude recorded at each receiver for each shot depends on the geology of the earth, and on the seismic source and receiver impulse responses. Geophysicists and geologists are interested in the variations of the impulse response of the earth. The impulse responses of the receivers and the source may vary, causing anomalous fluctuations of the amplitude recorded during the experiment. It is therefore necessary to correct for such fluctuations, when observed, in order to restore the earth component, which is the valuable information.
Figure 1 shows an amplitude plot in source and offset coordinates for a 2-D seismic survey provided by Mobil in 1994. For each shot and each offset position (i.e., for each trace of the survey) the value of the amplitude has been calculated by taking the root mean square of the trace amplitudes along the time axis. The global trend (low-frequency component of the earth) of the amplitude surface has been estimated by least-square fitting, and removed from the original surface to leave a globally flat 2-D amplitude map (Berlioux and Lumley, 1994).

|
|---|
|
amplitude
Figure 1. 2-D amplitude plot after removal of the global trend and normalization by the root-mean-square value. |
|
|
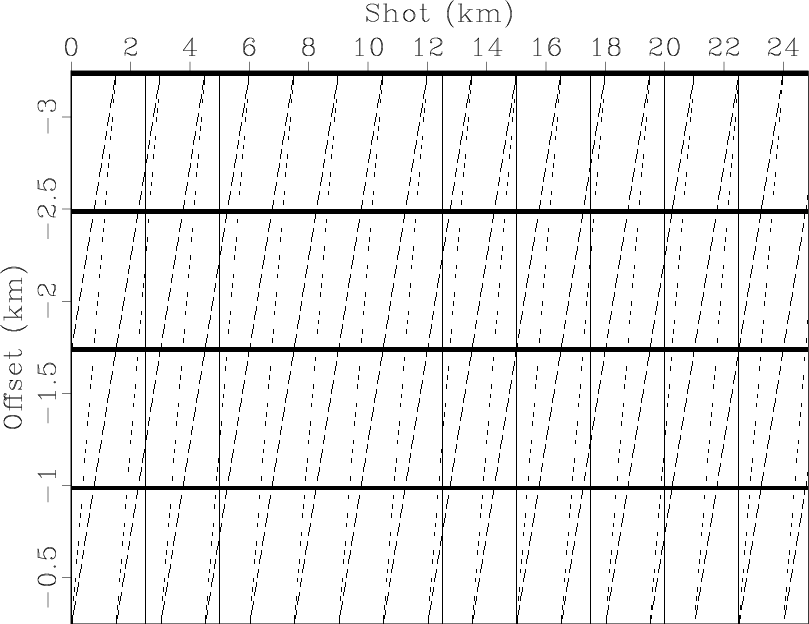
Figure 1 shows the result after normalization by the root-mean-square value of the amplitude. In this figure the horizontal stripes correspond to offsets where the hydrophone had an impulse response that was weaker (darker stripe) or stronger (brighter stripe) than the average response of the other receivers. Likewise, the vertical stripes indicate where the source had an impulse response that varied from the average. Less obvious, though noticeable, are two other categories of stripes dipping to the left. One is quite visible at the bottom of the plot around the offset -0.5 km, dipping at approximately 10 degrees. An example of the second type of stripe, which dips 20 degrees to the left, is visible at the source position 16 km. Based on the amplitude plot in Figure 1, we have built a model of offset-, source-, midpoint-, and receiver-consistent stripes (Figure 2). Comparing both figures we can identify the first category of dipping stripes as being midpoint-consistent, whereas the less steep stripes are receiver-consistent. The stripes in the receiver directions are broader than the others and therefore not as visible in the source and receiver coordinate system (Figure 3). The stripes in the offset direction follow the descending diagonal in the transformed coordinate system.
|
|---|
|
model
Figure 2. Model of offset-, source-, midpoint-, and receiver-consistent stripes, based on the 2-D amplitude plot in Figure 1. The solid dipping lines correspond to the receiver-consistent stripes, and the dotted lines represent the midpoint-consistent stripes. |
|
|

|
|---|
|
sramplitude
Figure 3. Portion of the amplitude map in Figure 1 displayed in the source and receiver space. The stripes along the descending diagonal follow the offset direction. Midpoint and receiver stripes are less visible in this coordinate system. |
|
|
Berlioux and Lumley (1994) and Lumley et al. (1995) proposed a method to estimate the source and offset correction coefficients in order to balance the amplitude of each trace in the survey. This method, based on a simple amplitude model, produces good results but does not take into account the receiver-consistent stripes still visible after correction. Because water has a substantially lower velocity than the underlying sediments, the waves travel nearly vertically in the water. The variations of the amplitude caused by the receiver can therefore be associated with near-surface anomalies or irregular sea-bottom topography that affects the receiver recording vertically above it. In the next section, we use a more complex amplitude model, which allows for these variations, and propose an iterative method to estimate the coefficients in order to later correct the amplitude map and balance each trace of the survey.
|
|
|
|
Iterative least-square inversion for amplitude balancing |